Back to C2 Home

4.b.1 - 2015 Q4 Answers

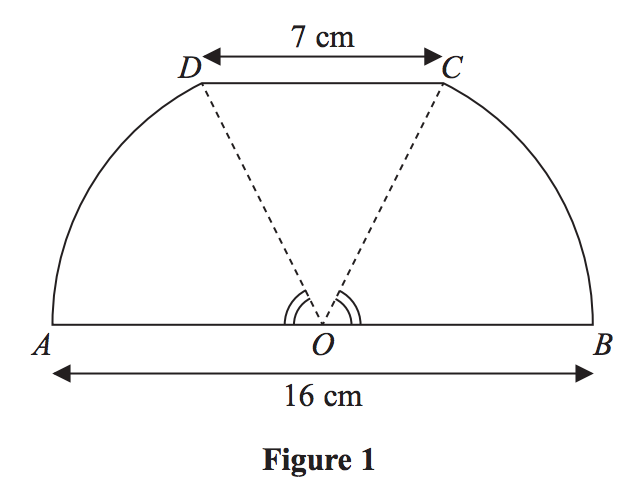
Figure 1 shows a sketch of a design for a scraper blade. The blade AOBCDA consists of an isosceles triangle COD joined along its equal sides to sectors OBC and ODA of a circle with centre O and radius 8 cm. Angles AOD and BOC are equal. AOB is a straight line and is parallel to the line DC. DC has length 7 cm.

(a) Show that the angle COD is 0.906 radians, correct to 3 significant figures. (2)

(b) Find the perimeter of AOBCDA, giving your answer to 3 significant figures. (3)

(c) Find the area of AOBCDA, giving your answer to 3 significant figures. (3)

Answers