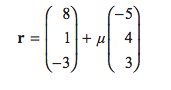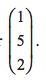??? - 2015 Q8
8. With respect to a fixed origin O, the line l1 is given by the equation
where ȝ is a scalar parameter.
The point A lies on l1 where ȝ = 1
(a) Find the coordinates of A. (1)
The point P has position vector
The point A lies on l1 where ȝ = 1
(a) Find the coordinates of A. (1)
The point P has position vector
The line l2 passes through the point P and is parallel to the line l 1
(b) Write down a vector equation for the line l2 (2)
(c) Find the exact value of the distance AP. Give your answer in the form k √2, where k is a constant to be determined. (2)
The acute angle between AP and l2 is θ.
(d) Find the value of cosθ (3)
A point E lies on the line l2 Given that AP = PE,
(e) find the area of triangle APE, (2)
(f) find the coordinates of the two possible positions of E. (5)
(b) Write down a vector equation for the line l2 (2)
(c) Find the exact value of the distance AP. Give your answer in the form k √2, where k is a constant to be determined. (2)
The acute angle between AP and l2 is θ.
(d) Find the value of cosθ (3)
A point E lies on the line l2 Given that AP = PE,
(e) find the area of triangle APE, (2)
(f) find the coordinates of the two possible positions of E. (5)