??? - 2016 Q7
8
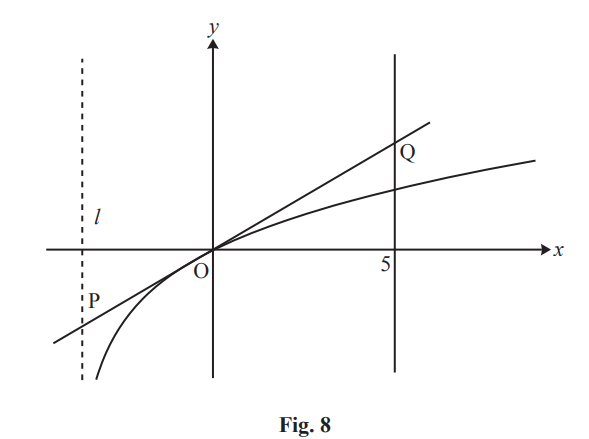
Fig. 8 shows the curve y=x/√ (x+4) and the line x = 5.
The curve has an asymptote l.
The tangent to the curve at the origin O crosses the line l at P and the line x = 5 at Q.
Fig. 8 shows the curve y=x/√ (x+4) and the line x = 5.
The curve has an asymptote l.
The tangent to the curve at the origin O crosses the line l at P and the line x = 5 at Q.
(i) Show that for this curve dy/dx = x+8/2(x+4)3/2 [5]
(ii) Find the coordinates of the point P. [4]
(iii) Using integration by substitution, find the exact area of the region enclosed by the curve, the tangent OQ and the line x = 5. [9]
(ii) Find the coordinates of the point P. [4]
(iii) Using integration by substitution, find the exact area of the region enclosed by the curve, the tangent OQ and the line x = 5. [9]