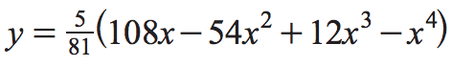??? - 2016 JUNE Q8
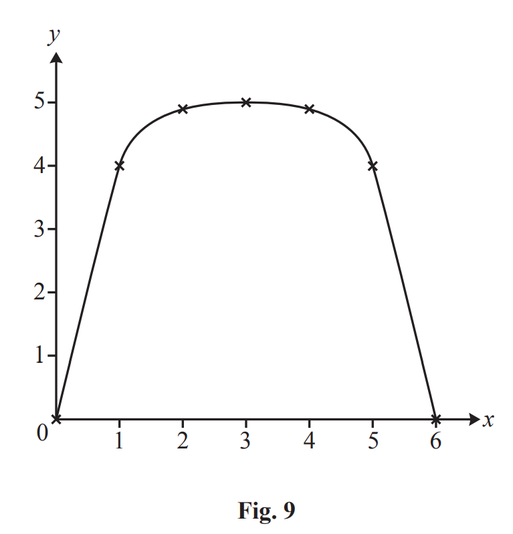
Fig. 9 shows the cross-section of a straight, horizontal tunnel. The x-axis from 0 to 6 represents the floor of the tunnel.
With axes as shown, and units in metres, the roof of the tunnel passes through the points shown in the table.
The length of the tunnel is 50m.
(i) Use the trapezium rule with 6 strips to estimate the area of cross-section of the tunnel. Hence estimate the volume of earth removed in digging the tunnel. [4]
(ii) An engineer models the height of the roof of the tunnel using the curve
(i) Use the trapezium rule with 6 strips to estimate the area of cross-section of the tunnel. Hence estimate the volume of earth removed in digging the tunnel. [4]
(ii) An engineer models the height of the roof of the tunnel using the curve
This curve is symmetrical about x = 3.
(A) Show that, according to this model, a vehicle of rectangular cross-section which is 3.6m wide and 4.4m high would not be able to pass through the tunnel. [2]
(B) Use integration to calculate the area of the cross-section given by this model. Hence obtain another estimate of the volume of earth removed in digging the tunnel. [5]
(A) Show that, according to this model, a vehicle of rectangular cross-section which is 3.6m wide and 4.4m high would not be able to pass through the tunnel. [2]
(B) Use integration to calculate the area of the cross-section given by this model. Hence obtain another estimate of the volume of earth removed in digging the tunnel. [5]