Back to Edexcel Maths Foundation November 2018 Paper 1 Home
Q17: Question – Paper 1 – November 2018
Q17: Question – Paper 1 – November 2018
Helpful Links
Question
Click here for a printable PDF of this question.
17)
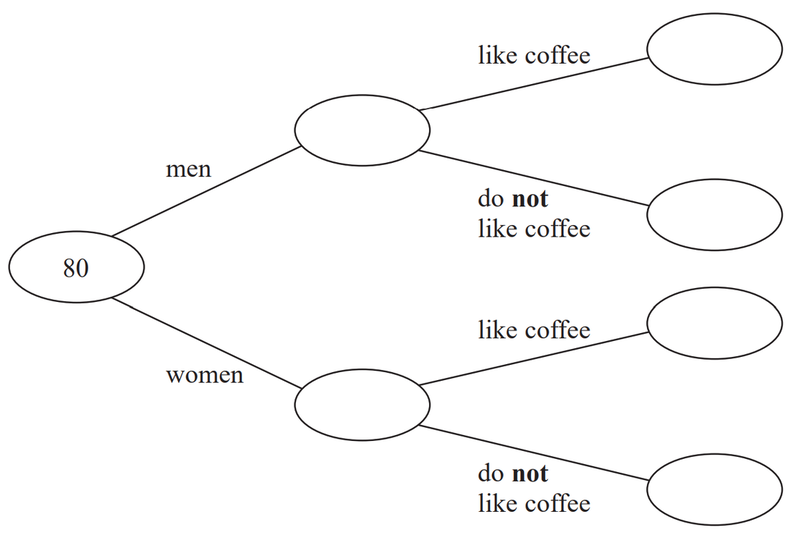
80 people are asked if they like coffee.
48 of these people are women.
61 of the 80 people like coffee.
8 of the men do not like coffee.
a) Use this information to complete the frequency tree.
17)
80 people are asked if they like coffee.
48 of these people are women.
61 of the 80 people like coffee.
8 of the men do not like coffee.
a) Use this information to complete the frequency tree.
[3 marks]
One of the people who like coffee is chosen at random.
b) Find the probability that this person is a woman.
[2 marks]