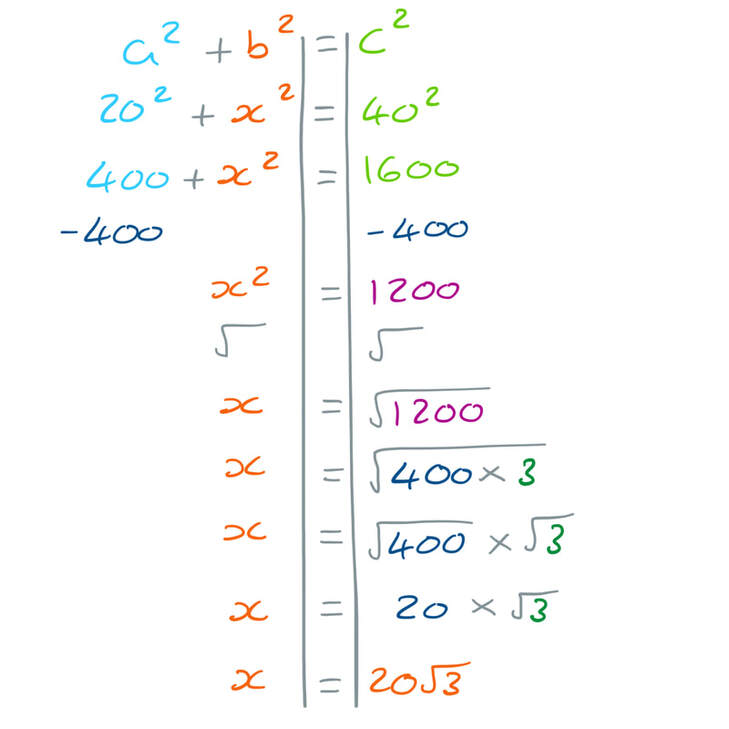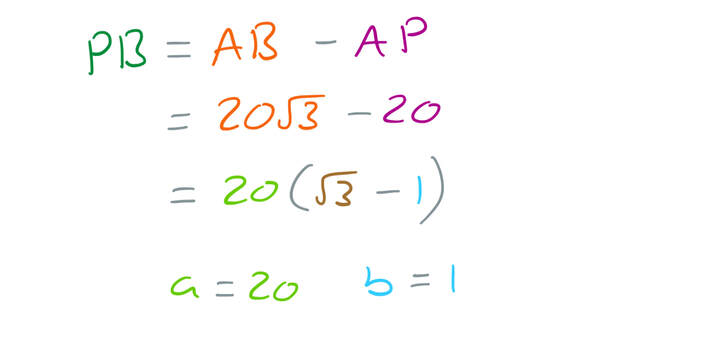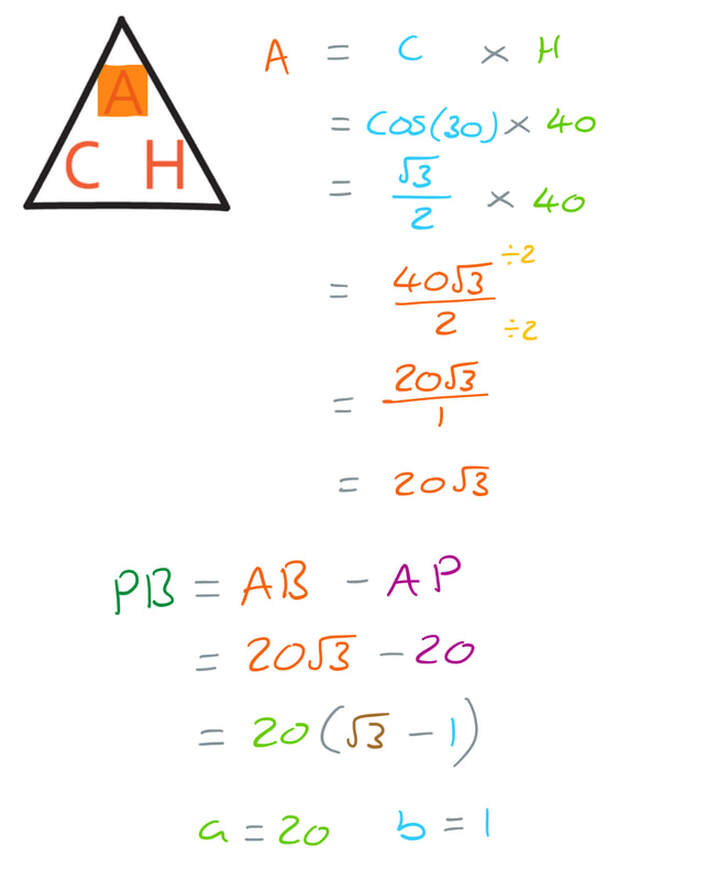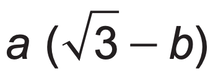Back to OCR Maths Higher November 2018 Paper 5 Home
​Q13: Answers – Paper 5 – November 2018

Helpful Links

Content:

• Exact Trigonometry Values
• Trigonometry – Finding a Side​
• Pythagoras: Not finding the Hypotenuse
• Simplifying Surds​

Quizzes:

• Exact Trig Values
• Trigonometry – Finding a Side
• Pythagoras: Not finding the Hypotenuse
• Simplifying Surds​

---

Mark Scheme

---

Working

---

Question

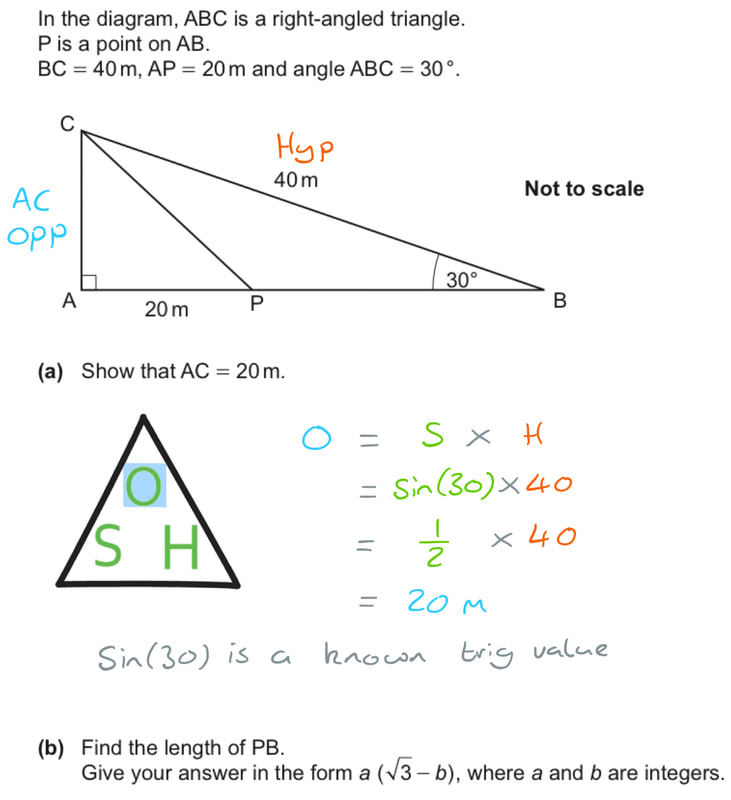
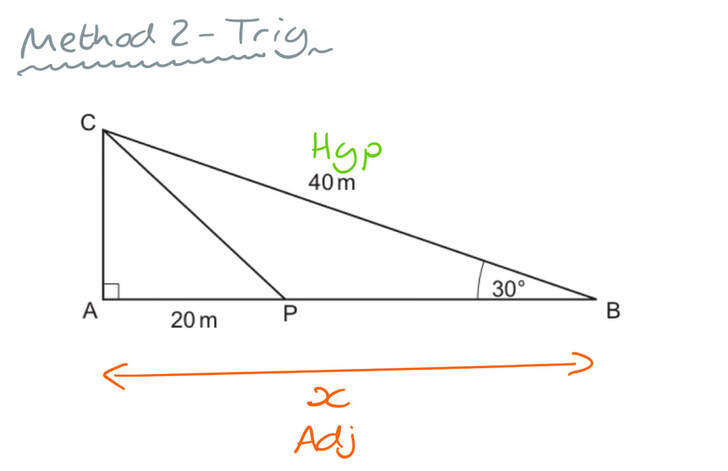
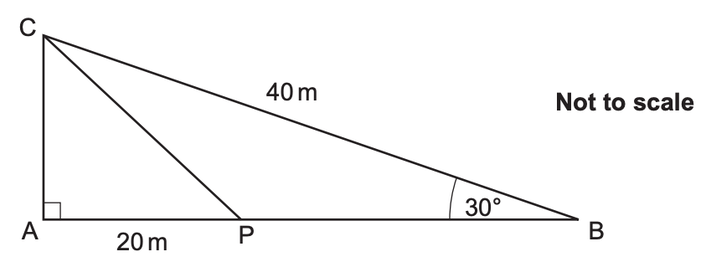
13) In the diagram, ABC is a right-angled triangle.
P is a point on AB.
​BC = 40m, AP = 20m and angle ABC = 30°.

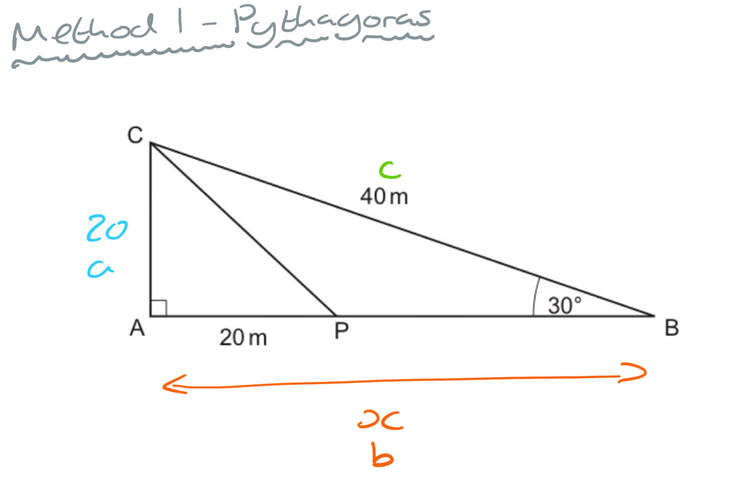
a) Show that AC = 20m.

[3 marks]

​b) Find the length of PB.
Give your answer in the form

where a and b are integers.

[3 marks]

Back to Question