Back to OCR Maths Higher November 2018 Paper 6 Home
Q6: Answers – Paper 6 – November 2018
Q6: Answers – Paper 6 – November 2018
Helpful Links
|
Content:
|
Mark Scheme
Working
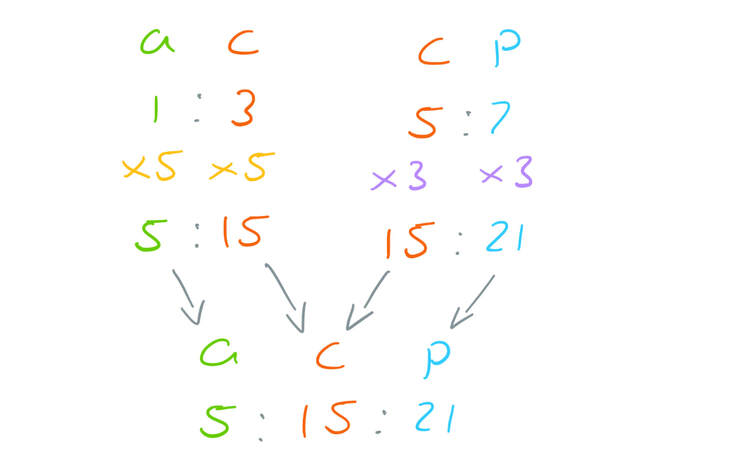
In a box of mixed nuts, the total number of almonds, cashews and peanuts is 1025.
The ratio of almonds to cashews is 1 : 3.
The ratio of cashews to peanuts is 5 : 7.
Calculate the number of cashews in the box.
In a box of mixed nuts, the total number of almonds, cashews and peanuts is 1025.
The ratio of almonds to cashews is 1 : 3.
The ratio of cashews to peanuts is 5 : 7.
Calculate the number of cashews in the box.
Question
6) In a box of mixed nuts, the total number of almonds, cashews and peanuts is 1025.
The ratio of almonds to cashews is 1 : 3.
The ratio of cashews to peanuts is 5 : 7.
Calculate the number of cashews in the box.
The ratio of almonds to cashews is 1 : 3.
The ratio of cashews to peanuts is 5 : 7.
Calculate the number of cashews in the box.
[4 marks]