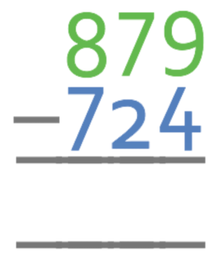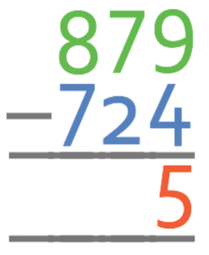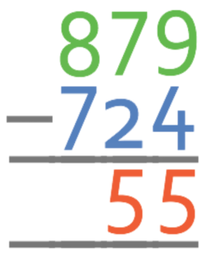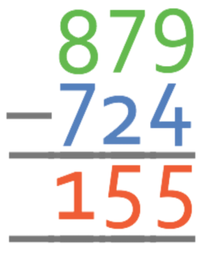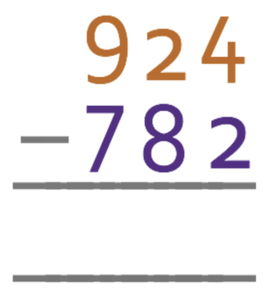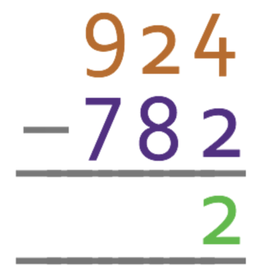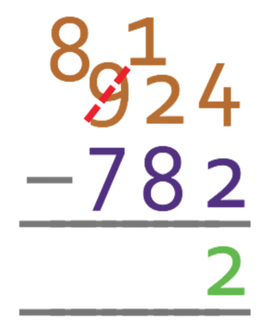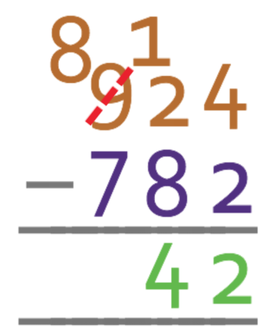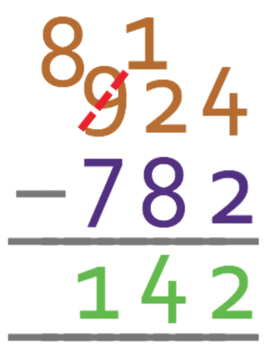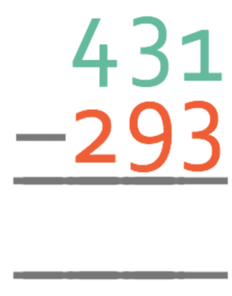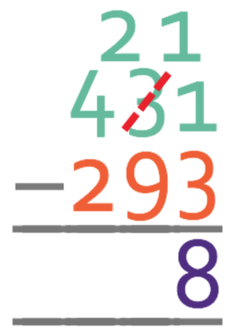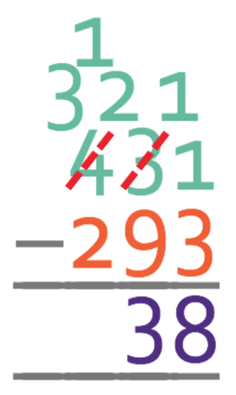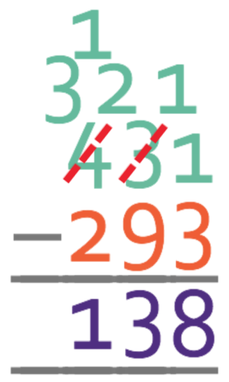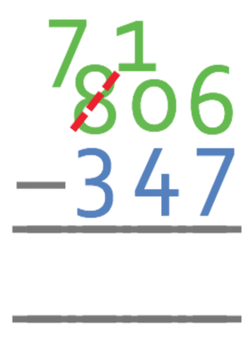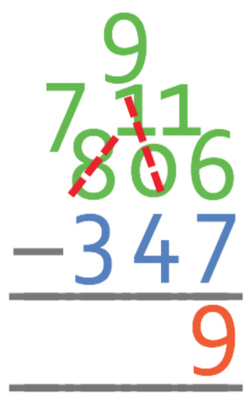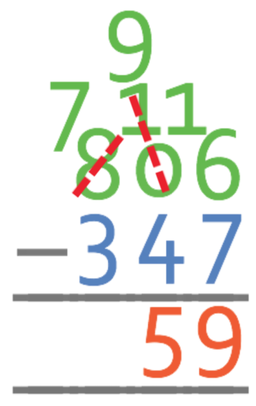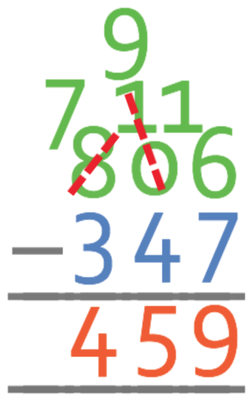Back to AQA Number (F) Home
1.1 E) Subtraction
1.1 E) Subtraction
Column subtraction is a very easy method to subtract numbers when we are unable to use a calculator. We write the number that we are subtracting below the number that we are subtracting the number from; for example, if we were column subtracting the calculation 879 – 724, we would write 724 below 879. When we are writing the numbers, we need to make sure that we line up all of the place values; we line all of the units up, the tens up, the hundreds up etc.
879 – 724 is written in column subtraction form below.
879 – 724 is written in column subtraction form below.
When we are column subtracting, we always start subtracting the smallest place value column; for integers (whole numbers), we subtract the units, then the tens, then the hundreds etc. If we are unable to subtract the values in one of the columns, we can borrow from the next place value to the left (example 2 and 3 will show borrowing taking place).
Example 1
Let’s now complete the calculation:
Let’s now complete the calculation:
We start with the units column; 9 – 4. This calculation can be done, which means that we do not need to borrow. Therefore, the units in the answer is 5.
We now move onto the next place value, which is the tens; 7 – 2. This can also be done, thus meaning that we do not need to borrow. 7 – 2 is 5, which means that we have 5 tens in the answer.
The final column is the hundreds column; 8 – 7. This can be done, which means that there is no need to borrow. There is 1 hundred in the answer.
Therefore, the answer is 155.
Example 2 – Borrowing
We are now going to have a look at an example that involves borrowing.
Complete the calculation:
We are now going to have a look at an example that involves borrowing.
Complete the calculation:
The first step is to line the place values up.
We then start subtracting the lowest place value, which for these two numbers is the units; the calculation is 4 – 2. This can be done, which means that there are 2 units in the answer.
We now move onto the next place value, which is the tens; 2 – 8. This will give a negative number, which means that we need to borrow from the next place value to the left in the top number. This means that we borrow 1 from the hundreds place value. The borrowing of 1 from the hundreds results in the 9 becoming an 8 in the hundreds column, and the 2 becoming a 12 in the tens column.
We are now able to take 8 from 12; 12 – 8 = 4. Therefore, we will have 4 tens in the answer.
We now move onto the hundreds column; 8 – 7. This gives 1, which means that there is 1 hundred in the answer.
Therefore, the answer to this question is 142.
Example 3 – Borrowing
Complete the calculation below:
Complete the calculation below:
Like all of the previous example, the first step is line the place values up.
We start by taking the units; 1 – 3. This is going to give us a negative number, which means that we need to borrow from the tens column. This means that the 3 in the tens column now becomes 2 and we have 11 in the units column. We are now able to complete the calculation; 11 – 3 = 8.
We now take the tens; 2 – 9. This will give us a negative number, which means that we need to borrow from the next place value in the top number, which is the hundreds. The 4 in the hundreds now becomes a 3, and there will now be 12 in the tens column. We are now able to complete the calculation; 12 – 9 = 3. There are 3 tens in the answer.
We now move onto the hundreds column; 3 – 2 = 1. This means that there will be a 1 in the hundred column in the answer.
Therefore, the answer to this question is 138.
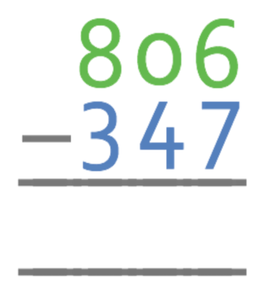
Example 4 – Borrowing Twice
We are now going to have a look at an example where we will need to borrow twice.
Complete the calculation below:
We are now going to have a look at an example where we will need to borrow twice.
Complete the calculation below:
Let’s write these numbers down with the place values lined up.
The first step is to take the units away from one another; 6 – 7. This give us a negative number, which means that we need to borrow from the next place value, which in this case is the tens. However, there are no tens in 806 to borrow from. Therefore, we borrow from the hundreds for the tens, and then borrow from the tens for the units. Currently there are 8 hundreds, and when we borrow from the hundreds, we will have 7 hundreds and 10 tens.
We now borrow from the tens for the units, which results in 9 tens and 16 units. We are now able to complete the calculation; 16 – 7 = 9.
We are now able to move onto the tens column; 9 – 4 = 5.
The final step is to work with the hundreds column; 7 – 3 = 4.
Therefore, the answer to this question is 459.
End Note
All of the numbers in the examples that we have looked at in this section have been whole numbers (integers). It may be the case that you are subtracting decimals. We column subtract decimals in exactly the same way that we have column subtracted whole numbers. We line all of the place values up and then start subtracting from the smallest place value. If we are unable to subtract the numbers in the place values, we borrow from the next place value to the left.
All of the numbers in the examples that we have looked at in this section have been whole numbers (integers). It may be the case that you are subtracting decimals. We column subtract decimals in exactly the same way that we have column subtracted whole numbers. We line all of the place values up and then start subtracting from the smallest place value. If we are unable to subtract the numbers in the place values, we borrow from the next place value to the left.