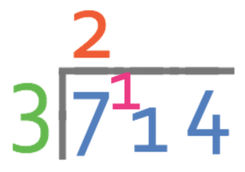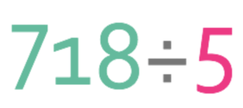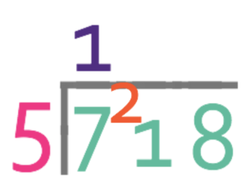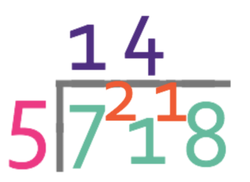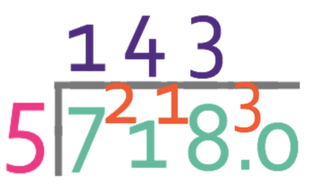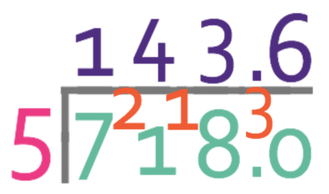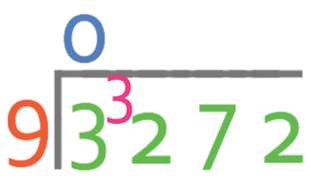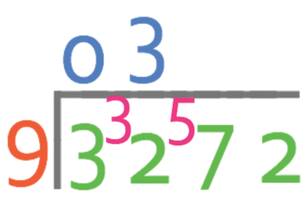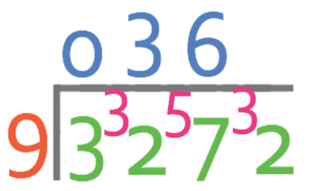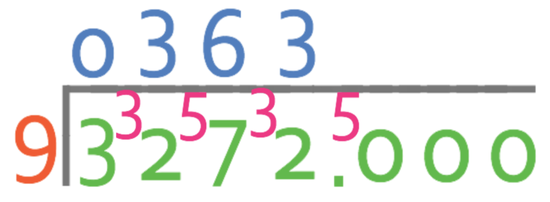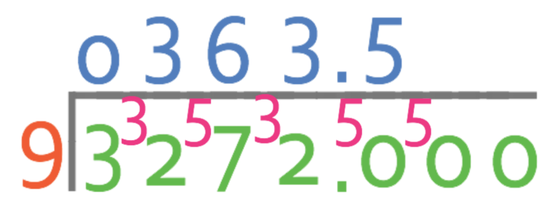Back to AQA Number (F) Home
1.1 H) Dividing – Bus Stop Method
1.1 H) Dividing – Bus Stop Method
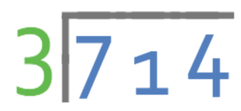
The bus stop method is a very good way to divide a very large number by a smaller number. With the bus stop method, we place the number that we are dividing inside the bus stop and the number that we are dividing by outside the bus stop. For example, if we were working out 714 ÷ 3, we would place 714 inside the bus stop and 3 outside the bus stop.
When we have the numbers in their correct places in the bus stop, we will divide the largest place value by the number outside the bus stop (we will always divide the first number inside the bus stop). For our example, we are dividing 7 by 3. The number of times that 3 fully goes into 7 is placed on top of the bus stop directly above the 7, and the remainder is placed next to the next place value in the number inside the bus stop. 3 fully goes into 7 2 times with a remainder of 1. Therefore, 2 is placed on top of the bus stop and the 1 is carried to the next place value.
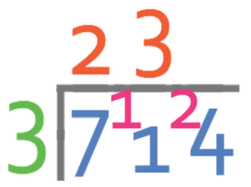
We are now seeing how many times 3 goes into 11, which it does 3 times with a remainder of 2. Therefore, we place a 3 on top of the bus stop above the tens place value and carry 2 to the next place value, which is the units.
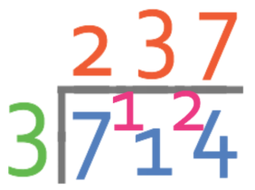
We are now onto the final place value, which is the units place value. We are seeing how many times 3 goes into 24, which it does 8 times with no remainder. Therefore, we place a 8 on top of the bus stop for the units place value.
The answer to 714 divided by 3 is 238.
Example 2 – Gives a Decimal
We are now going to have an example that will give us a decimal answer. The method used is exactly the same, but when we get to the units, we will get a remainder that will need to be carried into the tenth (the first decimal place) and the tenths for any whole number is 0; all of the decimal places for any whole number are 0.
Complete the calculation:
We are now going to have an example that will give us a decimal answer. The method used is exactly the same, but when we get to the units, we will get a remainder that will need to be carried into the tenth (the first decimal place) and the tenths for any whole number is 0; all of the decimal places for any whole number are 0.
Complete the calculation:
The number that we are dividing (718) is placed inside the bus stop and the number that we are dividing by (5) is placed outside the bus stop. I am just going to place 718 inside the bus stop without any decimal places because we can add them later (bearing in mind that when we are using the bus stop method, we will not know that our answer will be a decimal). The bus stop looks like what is given below.
We start with the highest place value. We are seeing how many times 5 goes into 7 (7 ÷ 5), which it goes in fully once with a remainder of 2. Therefore, we write 1 on top of the bus stop above the hundreds place value and carry the 2 to the next place value.
We are now seeing how many times 5 goes into 21 (21 ÷ 5), which it goes in fully 4 times with a remainder of 1. So, we write 4 on top of the bus stop above the tens place value and carry the 1.
We are now onto the units; we see how many times 5 goes into 18 (18 ÷ 5), which it goes in fully 3 times with a remainder of 3. As there is a remainder on the units, we carry the 3 into the tenth.
We are now dividing 30 by 5, which gives 6 with no remainder. As there is no remainder, there is nothing to carry on to the next place value.
Therefore, 718 ÷ 5 is 143.6.
Example 3 – Recurring Decimal
Complete the calculation below:
Complete the calculation below:
The first step is to set the bus stop up and start dividing.
We are seeing how many times 9 goes into 3 (9 ÷ 3). 9 does not go into 3, which means we place a 0 above the thousands and we carry the 3 to the next place value.
We are now looking at how many times 9 goes into 32, which it goes in fully 3 times with a remainder of 5. We write 3 above the bus stop and carry the 5 to the next place value.
The next step is to find out how many times 9 goes into 57, which it goes in fully 6 times with a remainder of 3.
We are now onto the units and are looking for how many times 9 goes into 32, which it goes in fully 3 times with a remainder of 5. As there is a remainder of 5 from the units place value, we need to carry the remainder to the tenth place value.
We are now looking for how many times 9 goes in to 50, which it goes in fully 5 times with a remainder of 5 (we carry the 5 to the hundredths).
We are now looking for how many times 9 goes into 50 (again), which it goes in fully 5 times with a remainder of 5.
This will keep continuing, so we can say that the answer is:
The dot on top of the 5 means recurring and this means that the 5 will keep repeating indefinitely (forever).
Ends Note
Sometimes you may be asked to give your answer to a certain number of decimal places. We answer questions like this by using the bus stop method to find the value to one more decimal place than we are asked to give our answer to. We then round our answer to the number of decimal places that we are asked in the question. For example, suppose that we are asked to round our answer to 1 decimal place, we would use the bus stop method to find the answer to 2 decimal places. We would then round our answer to 1 decimal place. For this example, we need to use the bus stop to 2 decimal places because the second decimal place effects the rounding of the answer to 1 decimal place.
Sometimes you may be asked to give your answer to a certain number of decimal places. We answer questions like this by using the bus stop method to find the value to one more decimal place than we are asked to give our answer to. We then round our answer to the number of decimal places that we are asked in the question. For example, suppose that we are asked to round our answer to 1 decimal place, we would use the bus stop method to find the answer to 2 decimal places. We would then round our answer to 1 decimal place. For this example, we need to use the bus stop to 2 decimal places because the second decimal place effects the rounding of the answer to 1 decimal place.