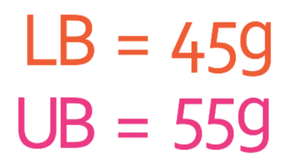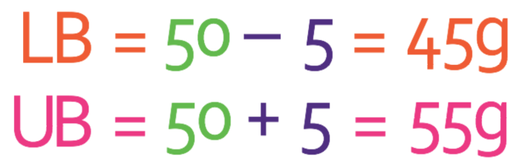Back to AQA Approximation (F) Home
1.2 F) Finding the Lower & Upper bound – Part 1
1.2 F) Finding the Lower & Upper bound – Part 1
Whenever we are given a number that has been rounded to a particular degree of accuracy (either to a particular place value or to a certain number of significant figures or another set value [such as to the nearest 5]), we can find the upper and lower bound to find the range of values that the number that has been rounded could have been between.
Example 1
Suppose that we have a chocolate bar that is 50g to the nearest 10 grams. Find the minimum mass (the lower bound) and maximum mass (the upper bound) of the chocolate bar.
There are two different methods to find the lower and upper bound of a number that has been rounded.
Method 1: Number Line
The first method that we are going to look at is a more visual method whereby we use a number line. We start by placing the rounded value on the number line, which in this case is 50 (I am going to ignore the units to make number line clearer).
Suppose that we have a chocolate bar that is 50g to the nearest 10 grams. Find the minimum mass (the lower bound) and maximum mass (the upper bound) of the chocolate bar.
There are two different methods to find the lower and upper bound of a number that has been rounded.
Method 1: Number Line
The first method that we are going to look at is a more visual method whereby we use a number line. We start by placing the rounded value on the number line, which in this case is 50 (I am going to ignore the units to make number line clearer).
The next step is to place the rounding values the are above and below 50g. 50g has been rounded to the nearest 10g. This means that the rounding value below is 40 g and the rounding value above is 60g. Therefore, we place 40 and 60 onto the number line.
The next step is to find the critical rounding values. We will have two critical rounding values. One will be half away between 40 and 50, and the other will be half away between 50 and 60. The two critical rounding values are 45 and 55.
These values are the critical rounding values because any number that is less than 45 will round down to 40, and any number that is between 45 and 50 will round up to 50. 45 is known as the lower bound.
This is similar for the 55. Any number that is less than 55 will round down to 55 and any number that is greater than 55 will round up to 60. Therefore, 55 is the upper bound.
From the lower and upper bound we can write what is known as the error interval. The error interval shows the range of possible values a rounded number can be. The error interval will always take the form of what is given below:
x in the inequality above is the value that we have rounded, which in this case would be the mass of the chocolate bar. For the mass of our chocolate bar, the error interval will be:
You may be wondering why the first sign is a “less than or equal to” sign and the second one is just a “less than”. This is because if our chocolate bar was 45g, it would round to 50g, thus meaning that the chocolate bar could be 45g. However, if the chocolate bar was 55g, it would round to 60g, which means that chocolate bar can be anything up to 55g, but it cannot be 55g because 55g would round up to 60g (for example the chocolate bar could be 54.9999999999g and this would round to 50g). Therefore, the second sign need to be just a “less than” sign and not a “less than or equal to sign” because it cannot equal to upper bound.
Method 2: ± Half the Degree of Accuracy
The second method involves finding the degree of accuracy that the number has been rounded to. When we have found the degree of accuracy, we then take half of the degree of accuracy off the rounded value to find the lower bound and add half the degree of accuracy onto the rounded value to find the upper bound.
For the chocolate example, the mass of the chocolate bar was rounded to the nearest 10g. This means that the degree of accuracy is 10. To find the lower bound, we take half of this off the rounded value, which tells us that the lower bound is 45 (50 – 5). To find the upper bound, we add half of the degree of accuracy onto the rounded value, which means that the upper bound is 55 (50 + 5).
Method 2: ± Half the Degree of Accuracy
The second method involves finding the degree of accuracy that the number has been rounded to. When we have found the degree of accuracy, we then take half of the degree of accuracy off the rounded value to find the lower bound and add half the degree of accuracy onto the rounded value to find the upper bound.
For the chocolate example, the mass of the chocolate bar was rounded to the nearest 10g. This means that the degree of accuracy is 10. To find the lower bound, we take half of this off the rounded value, which tells us that the lower bound is 45 (50 – 5). To find the upper bound, we add half of the degree of accuracy onto the rounded value, which means that the upper bound is 55 (50 + 5).
The lower and upper bound are exactly the same values as we obtained when we used the number line method. You should use whichever method you prefer to find the upper and lower bound. You may find it easier to use the number line method to start with to help you understand lower and upper bounds, but then as you become more confident, you will probably find it quicker and easier to use the second method.