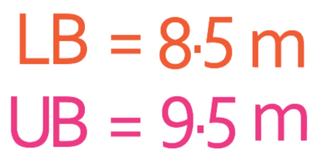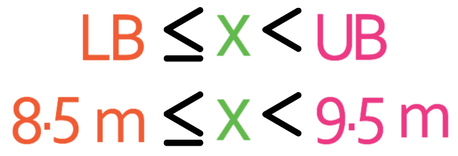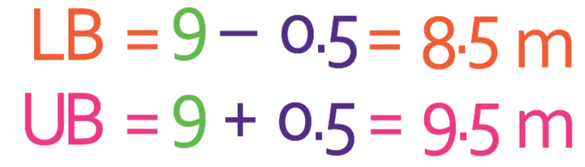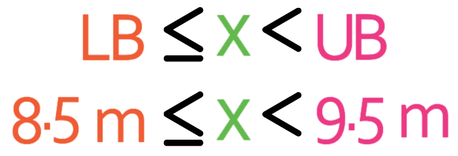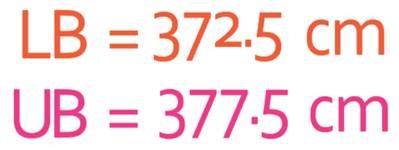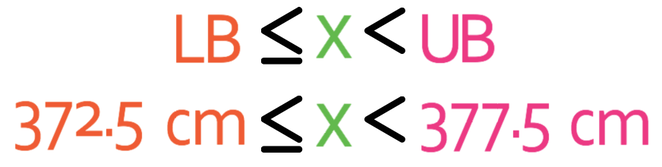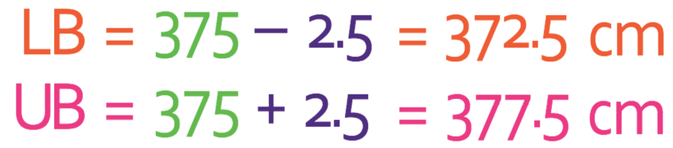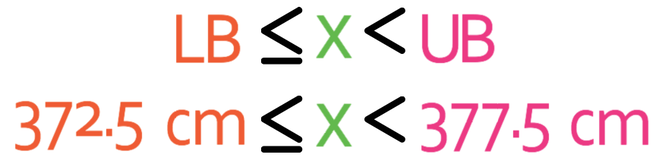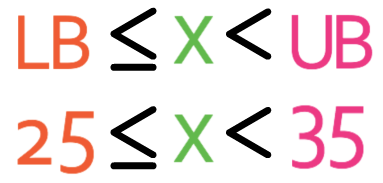Back to AQA Approximation (F) Home
1.2 G) Finding the Lower & Upper bound – Part 2
1.2 G) Finding the Lower & Upper bound – Part 2
The content in this section builds on the content that was looked at in the previous section. Make sure that you have gone through the content in the previous section before working through to the content in this section.
Example 1
A reel of ribbon is 9 m to the nearest metre. What is the lower and upper bound for the length of ribbon that I may get when I purchase a reel of this ribbon? Also, write the error interval.
Method 1: Number Line
The first step in this method is to draw out a number line with the rounded number on it; we place 9 on the number line (I am going to ignore units again). The next step is to place the rounding values that are above and below 9 m. The 9 m has been rounded to the nearest metre. Therefore, the value that is one rounding below is 8 (9 – 1) and the value that is one rounding above is 10 (9 + 1).
A reel of ribbon is 9 m to the nearest metre. What is the lower and upper bound for the length of ribbon that I may get when I purchase a reel of this ribbon? Also, write the error interval.
Method 1: Number Line
The first step in this method is to draw out a number line with the rounded number on it; we place 9 on the number line (I am going to ignore units again). The next step is to place the rounding values that are above and below 9 m. The 9 m has been rounded to the nearest metre. Therefore, the value that is one rounding below is 8 (9 – 1) and the value that is one rounding above is 10 (9 + 1).
The next step is to find the critical rounding values. One of the critical rounding values will be half away between 8 and 9, and the other critical rounding value will be half away between 9 and 10. The two critical rounding values are 8.5 and 9.5.
From the number line, we can see that the lower bound will be 8.5 m and the upper bound will be 9.5 m.
The final part of the question asks us to find the error interval, which we do by placing the lower and upper bound into the equation below. x in the equation below refers to the length of the ribbon.
Method 2: ± Half the Degree of Accuracy
The first step for this method is to work out what the degree of accuracy is for the ribbon. The length of the ribbon has been given to the nearest metre, which means that the degree of accuracy is 1 m. To obtain the lower bound for the ribbon, we take half of the degree of accuracy from the original value; we take 0.5 from 9, which means that the lower bound is 8.5 m (9 – 0.5). To find the upper bound of the length of ribbon, we add half of the degree of accuracy onto the original length of the ribbon, which means that the upper bound of the ribbon is 9.5 m (9 + 0.5).
The first step for this method is to work out what the degree of accuracy is for the ribbon. The length of the ribbon has been given to the nearest metre, which means that the degree of accuracy is 1 m. To obtain the lower bound for the ribbon, we take half of the degree of accuracy from the original value; we take 0.5 from 9, which means that the lower bound is 8.5 m (9 – 0.5). To find the upper bound of the length of ribbon, we add half of the degree of accuracy onto the original length of the ribbon, which means that the upper bound of the ribbon is 9.5 m (9 + 0.5).
We would then place these values into to the error interval formula.
Example 2
What is the lower and upper bound of 3.75 m to the nearest 5 cm? Also, write down the error interval.
Method 1: Number Line
We are told in this question that 3.75 m has been rounded to the nearest 5 cm. We have two different units here, which makes answering the question a little tricky. Therefore, the first step for this question is to covert both of these measurements into the same units. You could choose to do either of the units, but I think that it is considerable easier to have both of the units in cm. There are 100 cm in 1 metre, so we multiply the rounded length of the ribbon by 100; therefore, the rounded length of the ribbon is 375 cm (3.75 x 100). We are now ready to draw a number line with 375 cm on it.
What is the lower and upper bound of 3.75 m to the nearest 5 cm? Also, write down the error interval.
Method 1: Number Line
We are told in this question that 3.75 m has been rounded to the nearest 5 cm. We have two different units here, which makes answering the question a little tricky. Therefore, the first step for this question is to covert both of these measurements into the same units. You could choose to do either of the units, but I think that it is considerable easier to have both of the units in cm. There are 100 cm in 1 metre, so we multiply the rounded length of the ribbon by 100; therefore, the rounded length of the ribbon is 375 cm (3.75 x 100). We are now ready to draw a number line with 375 cm on it.
The next step is to place the rounding values that are above and below 375 cm. We were told in the question that 375 cm was rounded to the nearest 5 cm. Therefore, the rounding value below would be 370 cm and the rounding value above would be 380 cm.
We are now able to find the critical rounding values. The critical round values are 372.5 (half away between 370 and 375) and 377.5 (half away between 375 and 380).
From the number line, we can see that the lower bound is 372.5 cm and the upper bound is 377.5 cm.
As we have these values, we are able to place these into the error interval formula.
Method 2: ± Half the Degree of Accuracy
Like the method before, the first step would be to get both the rounded value and what we are rounding to into the same units. When they are both in cm, our rounded value if 375 cm and we are rounding to 5 cm.
The degree of accuracy for the value above is 5 cm. To find the lower bound for this value, we take half the degree of accuracy off of the rounded value; half of 5 cm is 2.5 cm. Therefore, the lower bound is 372.5 (375 – 2.5). In order to find the upper bound for this value, we add half the degree of accuracy onto the rounded value. Therefore, the upper bound is 377.5 (375 + 2.5).
Like the method before, the first step would be to get both the rounded value and what we are rounding to into the same units. When they are both in cm, our rounded value if 375 cm and we are rounding to 5 cm.
The degree of accuracy for the value above is 5 cm. To find the lower bound for this value, we take half the degree of accuracy off of the rounded value; half of 5 cm is 2.5 cm. Therefore, the lower bound is 372.5 (375 – 2.5). In order to find the upper bound for this value, we add half the degree of accuracy onto the rounded value. Therefore, the upper bound is 377.5 (375 + 2.5).
We would then place these values into the error interval formula to find the error interval.
Example 3 – Integers
An integer that has been rounded to the nearest 10 is 30. What is the lowest possible value and the highest possible value that this integer can be?
An integer is a whole number.
I am going to answer this question by finding the upper and lower bound for the number. I am going to work out the upper and lower bound by just using the number line method (feel free to use the other method to find the upper and lower bound). The first step in the number line method is to place 30 on the number line. The next step is to place the rounding values that are above and below 30 on the number line. The number has been rounded to the nearest 10, which means that the rounding value below is 20 (30 – 10) and the rounding value above is 40 (30 + 10).
An integer that has been rounded to the nearest 10 is 30. What is the lowest possible value and the highest possible value that this integer can be?
An integer is a whole number.
I am going to answer this question by finding the upper and lower bound for the number. I am going to work out the upper and lower bound by just using the number line method (feel free to use the other method to find the upper and lower bound). The first step in the number line method is to place 30 on the number line. The next step is to place the rounding values that are above and below 30 on the number line. The number has been rounded to the nearest 10, which means that the rounding value below is 20 (30 – 10) and the rounding value above is 40 (30 + 10).
We now need to find the critical values. The lower bound will be half away between 20 and 30, which means that the lower bound is 25. The upper bound will be half away between 30 and 40, which means that the upper bound is 35.
This tells us that the error interval is:
We were told at the start of the question that the number was an integer (whole number). We now need to look at the error interval to find the lowest and highest possible integers that the number could have been.
Let’s start by looking at the lower bound; 25 ≤ x. The sign for the lower bound is ≤, which means that that the number (x) is greater than or equal to 25. This means that the lowest possible value for the integer is 25.
Let’s now look at the upper bound; x < 35. The sign for the upper bound is <, which means that the number (x) is less than 35; the number cannot be 35. The first integer that is below 35 is 34, thus meaning that the greatest possible integer that this number can be is 34.
Therefore, the lowest number that this integer can be is 25 and the highest number that this integer can be is 34.
Let’s start by looking at the lower bound; 25 ≤ x. The sign for the lower bound is ≤, which means that that the number (x) is greater than or equal to 25. This means that the lowest possible value for the integer is 25.
Let’s now look at the upper bound; x < 35. The sign for the upper bound is <, which means that the number (x) is less than 35; the number cannot be 35. The first integer that is below 35 is 34, thus meaning that the greatest possible integer that this number can be is 34.
Therefore, the lowest number that this integer can be is 25 and the highest number that this integer can be is 34.