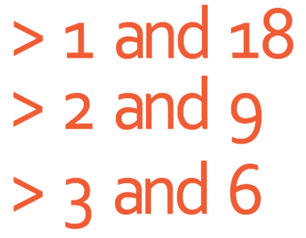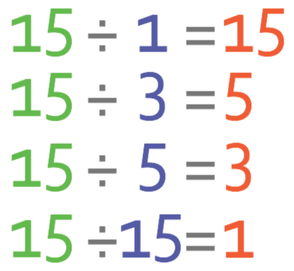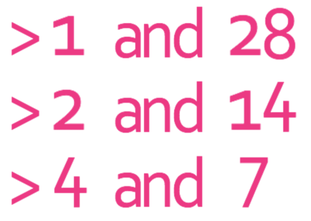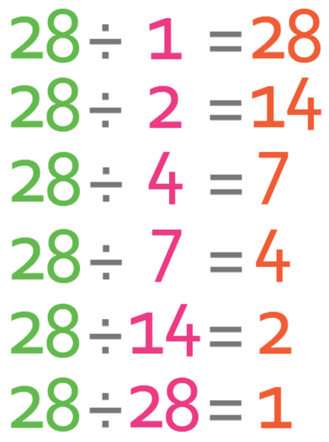Back to AQA Multiples & Factors (F) Home
1.4 A) Factor Pairs
1.4 A) Factor Pairs
Let’s start this section by working through a few different definitions.
- Multiples – these are the values that are in the times tables for that number. For example, the multiplies of 3 are 3, 6, 9, 12, 15 etc. The multiplies of 8 are 8, 16, 24, 32, 40 etc. There are an infinite number of multiplies of any given number.
- Factors – a factor is an integer (whole number) that a number can be divided by to give another integer. For example, 10 is a multiple of 20 because when you divide 20 by 10 we get the whole number 2. In addition to 10, there are many other factors for 20. The other factors are 1, 2, 4, 5, (10) and 20. When the number is divided by the factor, it must give an integer; there must be no remainder.
Factor Pairs
Sometimes it is useful to find all of the factors for a number. The easiest way to find all of the factors for a number is to use factor pairs. Factor pairs are pairs of numbers that multiply together to give the number that we are writing the factor pairs for.
For example, the factor pairs that make 20 are:
Sometimes it is useful to find all of the factors for a number. The easiest way to find all of the factors for a number is to use factor pairs. Factor pairs are pairs of numbers that multiply together to give the number that we are writing the factor pairs for.
For example, the factor pairs that make 20 are:
An example of where knowing factor pairs is useful is when we are factorising quadratic equations (click here to be taken through to the section on quadratic equations).
Factor pairs are also useful because we can use them to write out all of the factors of a particular number and the factor pairs ensure that we do not miss any factors out. This is because a factor must be multiplied by something else to give us the number that we are looking for the factors of.
The factors of 20 in ascending order are 1, 2, 4, 5, 10 and 20.
We are able to find the factor pairs for a number by dividing the number in question by 1, then 2, then 3 etc. If we obtain an integer when dividing, it means that we have a factor pair. We keep checking for factors until the next integer to be checked has already appeared in the list (this will make more sense in the examples).
Factor pairs are also useful because we can use them to write out all of the factors of a particular number and the factor pairs ensure that we do not miss any factors out. This is because a factor must be multiplied by something else to give us the number that we are looking for the factors of.
The factors of 20 in ascending order are 1, 2, 4, 5, 10 and 20.
We are able to find the factor pairs for a number by dividing the number in question by 1, then 2, then 3 etc. If we obtain an integer when dividing, it means that we have a factor pair. We keep checking for factors until the next integer to be checked has already appeared in the list (this will make more sense in the examples).
Example 1
Write down the factors of 18 by using factor pairs.
Let’s start by checking whether 1 is a factor of 18. We check whether it is a factor by dividing 18 by 1. 18 divided by 1 is 18, which means that 1 and 18 are factors. Therefore, the first factor pair is 1 and 18. 1 will always be a factor and so too will be the number that we are finding factors for, which in this case was 18. This is because anything divided by 1 is itself.
Write down the factors of 18 by using factor pairs.
Let’s start by checking whether 1 is a factor of 18. We check whether it is a factor by dividing 18 by 1. 18 divided by 1 is 18, which means that 1 and 18 are factors. Therefore, the first factor pair is 1 and 18. 1 will always be a factor and so too will be the number that we are finding factors for, which in this case was 18. This is because anything divided by 1 is itself.
Let’s now check 2. When we divide 18 by 2 we get 9, which is an integer. This means that another factor pair of 18 is 2 and 9.
We now do the same with 3. When 18 is divided by 3 we get 6, which is an integer, so another factor pair of 18 is 3 and 6.
Let’s now check 4. When 18 is divided by 4, we do not get an integer, and this means that 4 is not a factor of 18.
We now move on to check if 5 is a factor of 18. When 18 is divided by 5, we do not get an integer, which means that 5 is not a factor of 18.
The next number to check is 6. However, 6 has already appeared in the list; it appeared when 18 was divided by 3. Therefore, we stop checking because we have found all of the factor pairs. The factor pairs are:
We now move on to check if 5 is a factor of 18. When 18 is divided by 5, we do not get an integer, which means that 5 is not a factor of 18.
The next number to check is 6. However, 6 has already appeared in the list; it appeared when 18 was divided by 3. Therefore, we stop checking because we have found all of the factor pairs. The factor pairs are:
This means that the factors of 18 in ascending order are:
Example 2
Write down the factors of 15 by using factor pairs.
Like before, we are going to start by checking whether 1 is a factor. 1 is always a factor and when an integer is divided by 1, the outcome is the numbers that was being divided; 15 divided by 1 is 15. Therefore, the first factor pair is 1 and 15.
Write down the factors of 15 by using factor pairs.
Like before, we are going to start by checking whether 1 is a factor. 1 is always a factor and when an integer is divided by 1, the outcome is the numbers that was being divided; 15 divided by 1 is 15. Therefore, the first factor pair is 1 and 15.
The next factor to check is 2. When 15 is divided by 2, we do not obtain an integer, which means that 2 is not a factor of 15.
We now check whether 3 is a factor of 15, which it is because 15 divided by 3 is 5. Therefore, another factor pair for 15 is 3 and 5.
We now check whether 3 is a factor of 15, which it is because 15 divided by 3 is 5. Therefore, another factor pair for 15 is 3 and 5.
We now check 4. 4 is not a factor of 15 because 15 divided by 4 will not give a whole number.
The next number in the list to check is 5. However, 5 has already appeared in our factor pairs, which means that we stop checking for factor pairs because we have already found all of the factor pairs for 15.
This means that the factor pairs for 15 are:
The next number in the list to check is 5. However, 5 has already appeared in our factor pairs, which means that we stop checking for factor pairs because we have already found all of the factor pairs for 15.
This means that the factor pairs for 15 are:
Therefore, the factors of 15 in ascending order are:
Example 3
We can use the concepts of factor pairs and lists of factors to answer strange questions like this:
x is a positive integer.
15 ÷ x is a positive integer.
Work out the four possible values for x.
At the start of this section, we learnt that a factor is an integer (whole number) that a number can be divided by to give another integer. Therefore, x in this question will need to be a factor of 15 because when 15 is divided by x, an integer is obtained. From the previous question, we have learnt that the factors of 15 are 1, 3, 5 and 15. Therefore, the four possible values of x are 1, 3, 5 and 15. To prove that this is the case, I will sub all of these values in for x in “15 ÷ x” to check that we obtain a positive integer.
We can use the concepts of factor pairs and lists of factors to answer strange questions like this:
x is a positive integer.
15 ÷ x is a positive integer.
Work out the four possible values for x.
At the start of this section, we learnt that a factor is an integer (whole number) that a number can be divided by to give another integer. Therefore, x in this question will need to be a factor of 15 because when 15 is divided by x, an integer is obtained. From the previous question, we have learnt that the factors of 15 are 1, 3, 5 and 15. Therefore, the four possible values of x are 1, 3, 5 and 15. To prove that this is the case, I will sub all of these values in for x in “15 ÷ x” to check that we obtain a positive integer.
All of the values for x give a positive integer, which means that we have found the correct values for x; the four possible values of x are 1, 3, 5 and 15.
These types of questions do look quite complex, but they are actually fairly straight forward after you have seen a few of them. It may be worth getting this example and/ or the next example down on a revision card.
These types of questions do look quite complex, but they are actually fairly straight forward after you have seen a few of them. It may be worth getting this example and/ or the next example down on a revision card.
Example 4
y is a positive integer.
28 ÷ y is a positive integer.
Work out the six possible values for y.
The first step in answering this question is to find all of the factors of 18. I am going to find these factors by using factor pairs. The factor pairs for 28 are:
y is a positive integer.
28 ÷ y is a positive integer.
Work out the six possible values for y.
The first step in answering this question is to find all of the factors of 18. I am going to find these factors by using factor pairs. The factor pairs for 28 are:
Therefore, the factors of 28 are 1, 2, 4, 7, 14 and 28. These values are the possible values for y. Just to prove that this is the case, I will sub these values in for y into “28 ÷ y”.
All of these values for y work, which means that the values for y that we found are correct; the six possible values for y are 1, 2, 4, 7, 14 and 28.
Also, you may have noticed that when we checked a particular y value, we obtained the other number that was in the factor pair. For example, when we subbed y in as 2 into “28 ÷ y”, we obtained 14, which was the other number in the factor pair; the factor pair was 2 and 14.
Also, you may have noticed that when we checked a particular y value, we obtained the other number that was in the factor pair. For example, when we subbed y in as 2 into “28 ÷ y”, we obtained 14, which was the other number in the factor pair; the factor pair was 2 and 14.