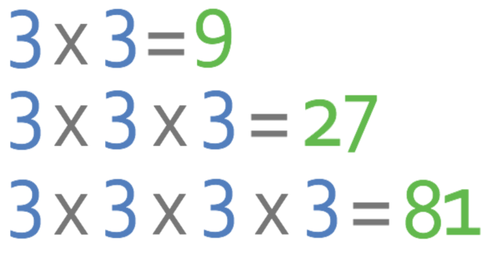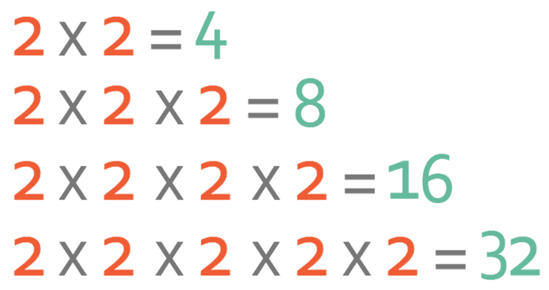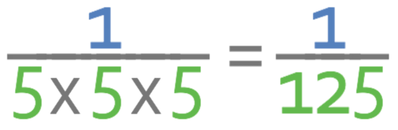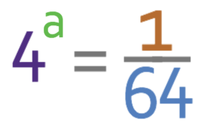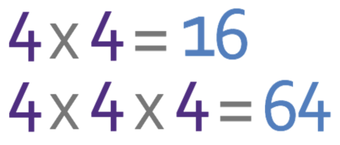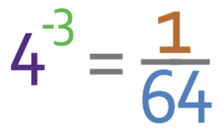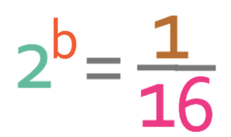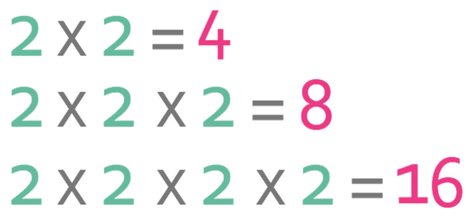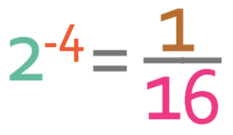Back to AQA Indices (F) Home
1.6 G) Putting Numbers into Indices – Part 1
1.6 G) Putting Numbers into Indices – Part 1
It may be the case that you are asked to find the power for an index number. Questions like this look very complex but they are actually fairly straightforward. We are going to have a few examples in this section and the next section.
Example 1
81 can be written in the form of 3x where x is an integer (whole number). Find the value of x.
This question is essentially saying “3 to the power of what is 81”. The easiest way to answer this question is to keep multiplying 3 by itself until we get 81. The working for this is shown below:
From the above working, we can see that 3 has been multiplied 4 times and this means that x is 4.
Example 2
We have the equation below:
We have the equation below:
Find the value of y.
This question is essentially saying “2 to the power of what is 32”. We answer this question in exactly the same way as the previous question; we keep multiplying 2 by itself until we get 32. The working is shown below:
This question is essentially saying “2 to the power of what is 32”. We answer this question in exactly the same way as the previous question; we keep multiplying 2 by itself until we get 32. The working is shown below:
From the above working, we can see that 2 has been multiplied 5 times and this means that y is 5.
Negative Powers
Negative powers can make these types of questions more complex. Before we go through a few examples, let’s just remind ourselves of the rules regarding negative powers.
When we take an index number out of a negative power, we reciprocate the index number and change the sign of the power from negative to positive. Reciprocating the number means dividing 1 by the index number.
For example, what is:
Negative powers can make these types of questions more complex. Before we go through a few examples, let’s just remind ourselves of the rules regarding negative powers.
When we take an index number out of a negative power, we reciprocate the index number and change the sign of the power from negative to positive. Reciprocating the number means dividing 1 by the index number.
For example, what is:
The power is -3, which is negative. Therefore, we reciprocate the index number (divide 1 by the index number) and change the sign of the power from negative to positive (the power changes from -3 to 3).
We now work out what 53 is.
Therefore, 5-3 is 1/125.
We are now going to have a look at some questions that require us to work backwards.
Example 3
We have the equation below:
We have the equation below:
Find the value of a.
The right side of the above equation is a fraction, which means that we are going to have a negative power; a will be negative.
Now that we know that a is negative, we can ignore the fraction and find the value of a that gives us 64. I am going to find the value of a by using the same process as the process that we used in example 1 and 2; we keep multiplying 4 by itself until we get 64. The working is shown below:
The right side of the above equation is a fraction, which means that we are going to have a negative power; a will be negative.
Now that we know that a is negative, we can ignore the fraction and find the value of a that gives us 64. I am going to find the value of a by using the same process as the process that we used in example 1 and 2; we keep multiplying 4 by itself until we get 64. The working is shown below:
From the above working, we can see that 4 is multiplied 3 times.
We now combine this with the negative sign to get -3. This means that a is -3.
We now combine this with the negative sign to get -3. This means that a is -3.
Example 4
We have the equation below:
We have the equation below:
Find the value of b.
The right side of the above equation is a fraction, which means that we are going to have a negative power; b will be negative.
Now that we know that b is negative, we can ignore the fraction and find the value for b that gives us 16. We do this by multiplying 2 by itself until we get 16. The working is shown below:
The right side of the above equation is a fraction, which means that we are going to have a negative power; b will be negative.
Now that we know that b is negative, we can ignore the fraction and find the value for b that gives us 16. We do this by multiplying 2 by itself until we get 16. The working is shown below:
From the above working, we can see that 2 is multiplied 4 times.
We now combine this with the negative sign to get -4. This means that b is -4.
We now combine this with the negative sign to get -4. This means that b is -4.