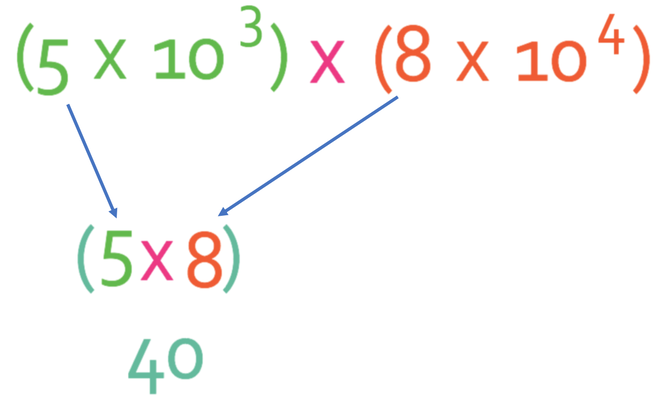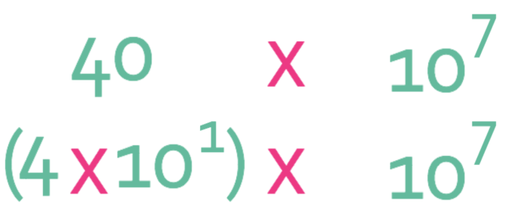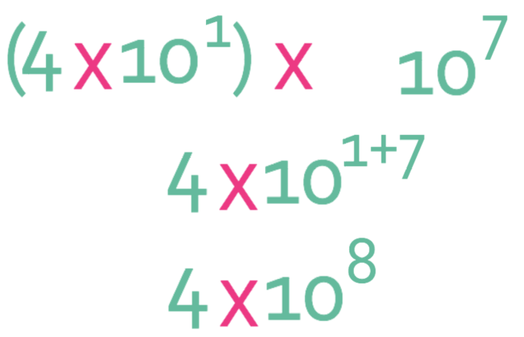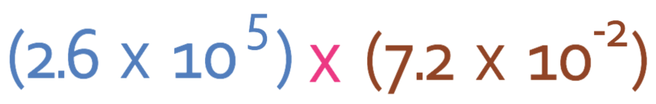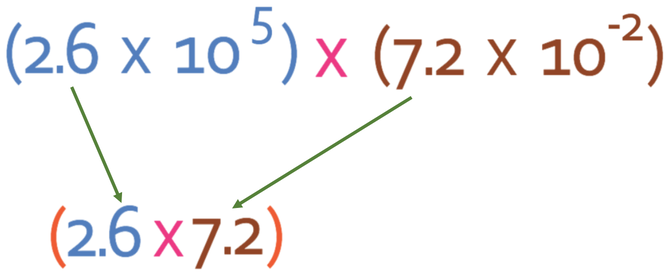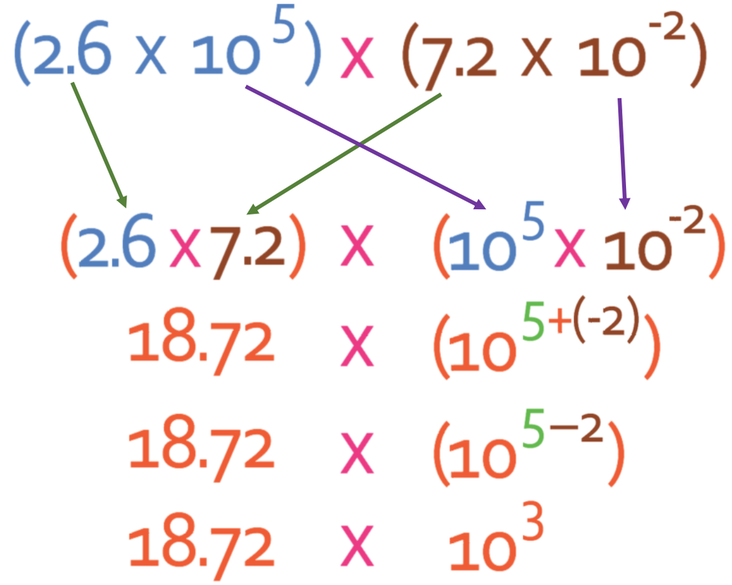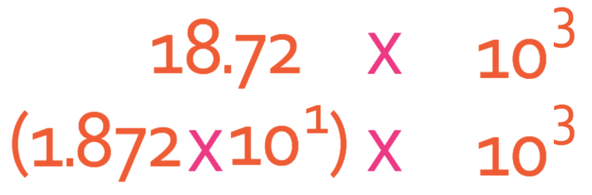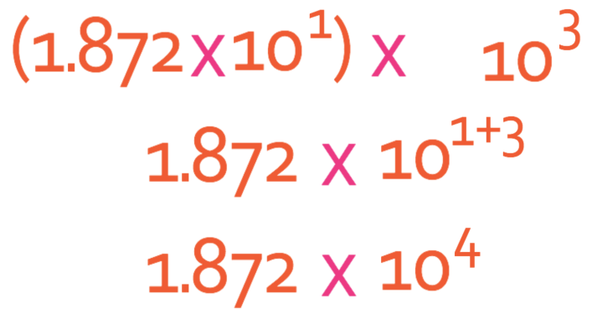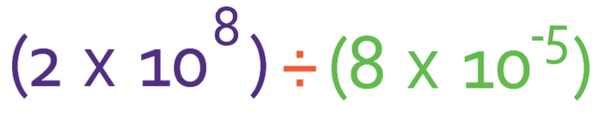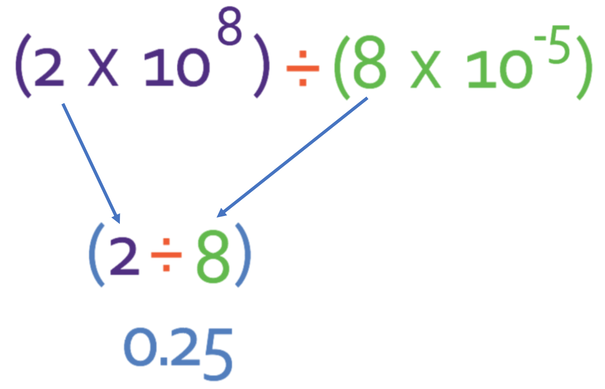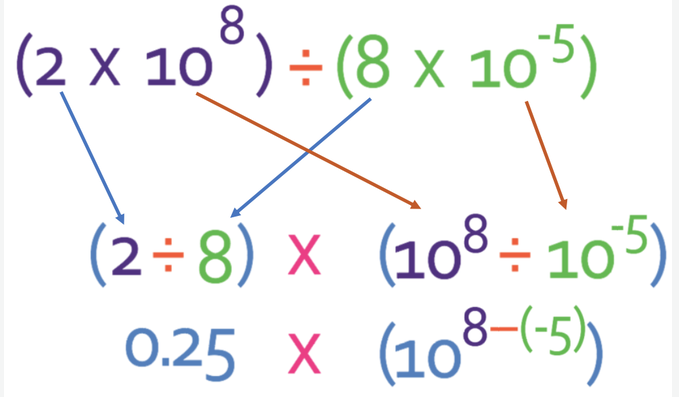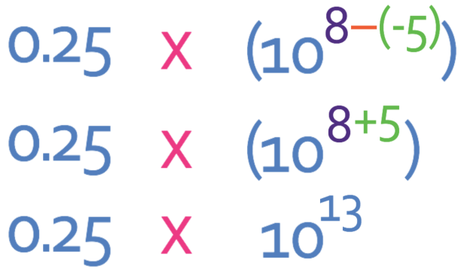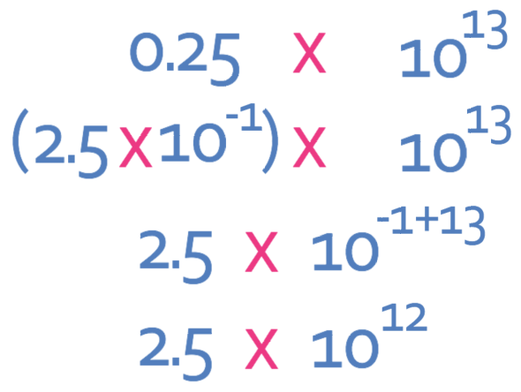Back to AQA Standard Form (F) Home
​​1.7 D) ​Multiplying & Dividing

There are two steps for multiplying and dividing numbers that are in standard form. These two steps are:

 

Step 1

Multiply or divide the numbers

 

Step 2

Apply the laws of indices to the powers of 10. When we are multiplying powers together we add the powers. For example; 10⁴ x 10⁷ = 10⁴⁺⁷ = 10¹¹. When we are dividing powers, we subtract the powers. For example; 10⁸ ÷ 10⁵ = 10^8-5 = 10³. (Note: these laws only apply if the base number is the same. In these examples, the base numbers were 10 and this will always be the case for numbers that are written in standard form. We are not be able to add or take the powers if the bases were not the same; for example, we could not add the powers for 5⁷ x 6⁴).

---

Example 1

What is:

The first step is to multiply the numbers

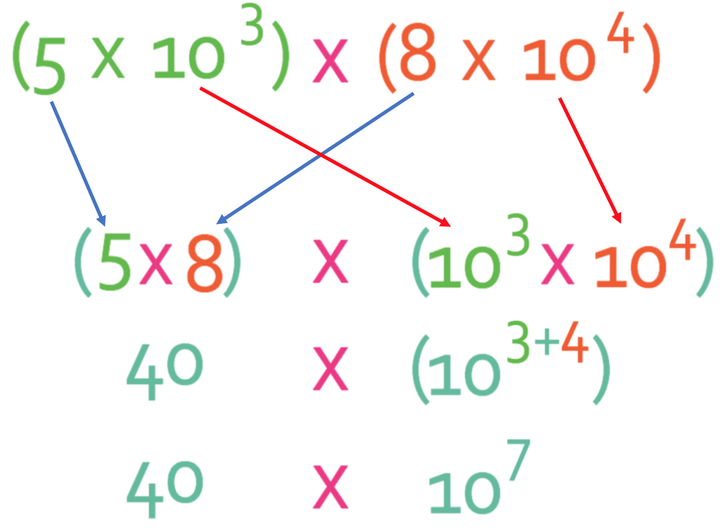
The next step is to multiply the powers (we are multiplying, so we add the powers together);

This answer is not in standard form because 40 is greater than 10 (remember that A must satisfy 1 ≤ A < 10). Therefore, we need to re-adjust the answer. The best way to re-adjust the answer is to get the number part of the answer (the 40) into standard form and then combine the powers of 10. 40 in standard form is 4 x 10¹ (note: the 1 is not necessary, but it is useful to keep it as it helps us when we are combining the powers of 10).

We now combine the 10’s; 10¹ x 10⁷. We are multiplying power with the same base. Therefore, we add the powers.

Therefore, the final answer to this question is 4 x 10⁸.

---

Example 2

What is:

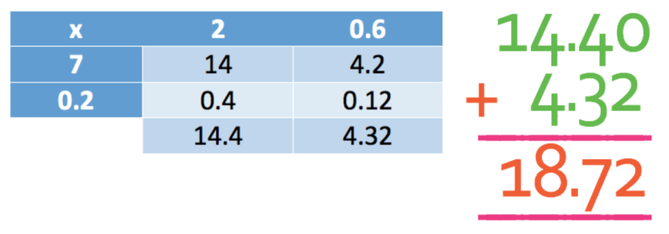
The first step is to multiply out the numbers; 2.6 x 7.2.

I am going to multiply these numbers out using the grid method. If you do not like the grid method, you could multiply the numbers out by using the column method. Click here to be taken to the sections that explore the grid method and column method in more detail. 

The next step is to multiply the powers (we are multiplying powers with the same base, so we add the powers).

Currently this answer is not in standard form and this is because 18.72 is not between 1 and 10. Therefore, we need to get the number part of this answer into standard form.

The next step is to combine the powers of 10; 10¹ x 10³. We add the powers because we are multiplying powers with the same base.

Therefore, the answer to this question is 1.872 x 10⁴.

---

Example 3

Let’s now have a division example. What is:

Like the multiplication example, we divide the number first; 2 ÷ 8 = ²/₈ = ¹/₄ = 0.25. A in the final answer will be a number rather than a fraction. Therefore, it is easier to write our answer for the numbers as a decimal.

The next step is to apply the laws of indices to the powers of 10 (we are dividing powers with the same base, so we take the powers). We need to be careful with the signs on the powers; taking a negative becomes a positive, so taking -5 becomes adding 5.

The taking of a negative number results in you adding that number. This means that 8 – (-5) becomes 8 + 5, which is 13.

0.25 is not between 1 and 10, which means that we need to re-adjust the answer. The best way to re-adjust the answer is to get the first part (0.25) into standard form and then combine the powers.

Therefore, the answer to this question is 2.5 x 10¹²