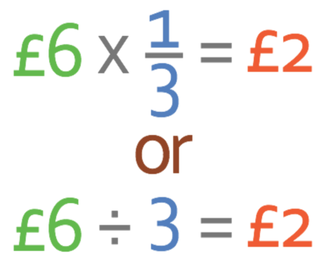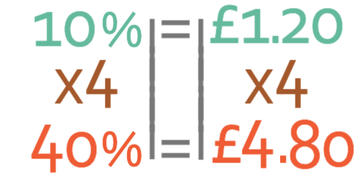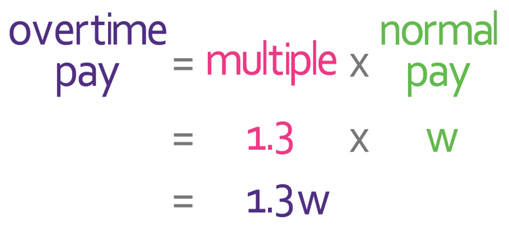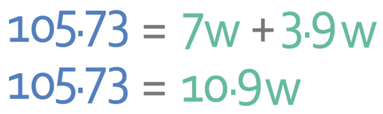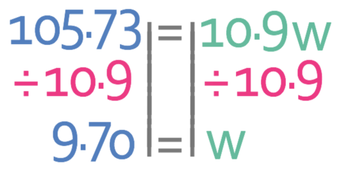Back to AQA Financial Maths (F) Home
1.8 C) Overtime
1.8 C) Overtime
Sometimes individuals who are paid hourly can get paid more money per hour for working above a certain number of hours, or for working antisocial hours (such as nights). This is known as overtime.
Sometimes you will be given the overtime as a multiply of normal pay; for example, “overtime pay is 1.3 times normal pay”. Other times, you will be given the difference in overtime pay to normal pay as a percentage or a fraction; for example, “overtime pay is 40% more than normal pay”.
Whenever we are working out wages when we have normal and overtime pay, we need to be careful that we are multiplying the number of hours worked at each pay rate by their respective pay rate.
Sometimes you will be given the overtime as a multiply of normal pay; for example, “overtime pay is 1.3 times normal pay”. Other times, you will be given the difference in overtime pay to normal pay as a percentage or a fraction; for example, “overtime pay is 40% more than normal pay”.
Whenever we are working out wages when we have normal and overtime pay, we need to be careful that we are multiplying the number of hours worked at each pay rate by their respective pay rate.
Example 1
An individual gets paid £6 per hour. For working overtime, our individual gets paid a third more than their normal pay. What is the overtime hourly wage?
We are told that the individual gets paid a third more than their normal pay for working overtime. Therefore, we find what a third of their normal wage is and add the third onto the normal wage. Their normal wage is £6 and we find out what a third of £6 is by either multiplying by a third or dividing by 3.
An individual gets paid £6 per hour. For working overtime, our individual gets paid a third more than their normal pay. What is the overtime hourly wage?
We are told that the individual gets paid a third more than their normal pay for working overtime. Therefore, we find what a third of their normal wage is and add the third onto the normal wage. Their normal wage is £6 and we find out what a third of £6 is by either multiplying by a third or dividing by 3.
A third of normal pay is £2. We now add this (£2) onto the normal rate of pay (£6) to find the overtime rate of pay.
Therefore, our individual gets paid £8 per hour of overtime.
Example 2
An individual works a 13-hour shift. His normal rate of pay is £12 per hour. However, if the individual works over 8 hours, he earns 40% more for each additional hour above 8 hours worked. How much money does our individual get paid for the 13-hour shift? This question is non-calculator.
This question contains percentages, click here to be taken through to the percentage section.
The first step in this question is to work out the number of hours that our individual works at a normal wage and the number of hours that our individual works at an overtime wage. The question tells us that the first 8 hours of a shift is paid at a normal wage and any additional hours over 8 hours receives the overtime rate of pay. Our individual is working for 13 hours, which means that he will receive 8 hours at normal pay and 5 hours at the overtime pay (13 – 8 = 5).
The question tells us that the normal rate of pay is £12 and that he earns 40% more for overtime. The question is non-calculator. Therefore, the best way to find out what 40% of £12 is, is to find out what 10% is and then multiply it by 4 to get what 40% is. We find what 10% of £12 is by dividing by 10.
An individual works a 13-hour shift. His normal rate of pay is £12 per hour. However, if the individual works over 8 hours, he earns 40% more for each additional hour above 8 hours worked. How much money does our individual get paid for the 13-hour shift? This question is non-calculator.
This question contains percentages, click here to be taken through to the percentage section.
The first step in this question is to work out the number of hours that our individual works at a normal wage and the number of hours that our individual works at an overtime wage. The question tells us that the first 8 hours of a shift is paid at a normal wage and any additional hours over 8 hours receives the overtime rate of pay. Our individual is working for 13 hours, which means that he will receive 8 hours at normal pay and 5 hours at the overtime pay (13 – 8 = 5).
The question tells us that the normal rate of pay is £12 and that he earns 40% more for overtime. The question is non-calculator. Therefore, the best way to find out what 40% of £12 is, is to find out what 10% is and then multiply it by 4 to get what 40% is. We find what 10% of £12 is by dividing by 10.
We want to know what 40% is so we multiply what 10% is by 4.
The final step to find out the overtime pay is to add this 40% onto the normal rate of pay.
Therefore, our individual gets paid £16.80 for every additional hour worked over 8 hours.
We now have everything that we need to find out how much our individual earns from this 13-hour shift.
We now have everything that we need to find out how much our individual earns from this 13-hour shift.
When we are multiplying by 5, you may find it easier to multiply by 10 and then half the results. When we multiply £16.80 by 10, we get £168. We then need to divide by 2, which gives us £84.
Therefore, our worker earns £180 for his 13-hour shift.
Example 3
I work at a restaurant for 10 hours. Out of these 10 hours, 7 hours are at the normal rate of pay and 3 hours are at the overtime rate of pay. Overtime pay is 1.3 times the normal rate of pay. I earn £105.73 for working for 10 hours. What is the normal rate of pay?
The first step in answering this question is to let the normal rate of pay be an unknown and the unknown that I am going to choose is w. We are told in the question that the overtime rate of pay is 1.3 times the normal rate of pay. As we have just let the normal rate of pay be w, we can find the overtime rate of pay by multiplying the normal rate of pay (w) by 1.3; this results in the overtime rate of pay being 1.3w.
I work at a restaurant for 10 hours. Out of these 10 hours, 7 hours are at the normal rate of pay and 3 hours are at the overtime rate of pay. Overtime pay is 1.3 times the normal rate of pay. I earn £105.73 for working for 10 hours. What is the normal rate of pay?
The first step in answering this question is to let the normal rate of pay be an unknown and the unknown that I am going to choose is w. We are told in the question that the overtime rate of pay is 1.3 times the normal rate of pay. As we have just let the normal rate of pay be w, we can find the overtime rate of pay by multiplying the normal rate of pay (w) by 1.3; this results in the overtime rate of pay being 1.3w.
We are now able to sub in the values that we know into the equation below. We know the normal hours worked (7), the overtime hours worked (3 [10 – 7 = 3]) and both the normal and overtime rate of pay. I am going to ignore units as it makes the working easier to understand.
We can multiply these out and collect like terms.
We want to find what w is and not what 10.9w is. Therefore, we need to divide both sides of the equation by 10.9.
Therefore, we can see that the normal rate of pay is £9.70.
Extra Points
It may be the case that in a question like this you are given the overtime rate of pay as a percentage increase on the normal rate of pay; for example, “overtime pay is 60% more than normal pay”. If this is the case, you should turn the percentage into a multiplier.
For the above example, we are told that overtime pay is 60% higher than normal pay. Normal pay is 100% and overtime pay is 60% higher. Therefore, we add 60% to 100%, which means that overtime pay is 160%.
Extra Points
It may be the case that in a question like this you are given the overtime rate of pay as a percentage increase on the normal rate of pay; for example, “overtime pay is 60% more than normal pay”. If this is the case, you should turn the percentage into a multiplier.
For the above example, we are told that overtime pay is 60% higher than normal pay. Normal pay is 100% and overtime pay is 60% higher. Therefore, we add 60% to 100%, which means that overtime pay is 160%.
The next step is to convert 160% into a multiplier, which we do by dividing by 100.
From the working above, you can see that overtime pay is 1.6 times normal pay. If we let w be normal pay, overtime pay would be 1.6w (1.6 x w).