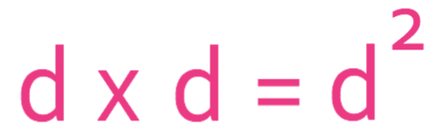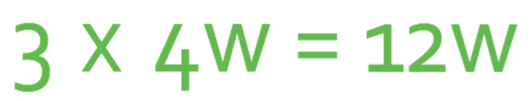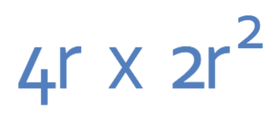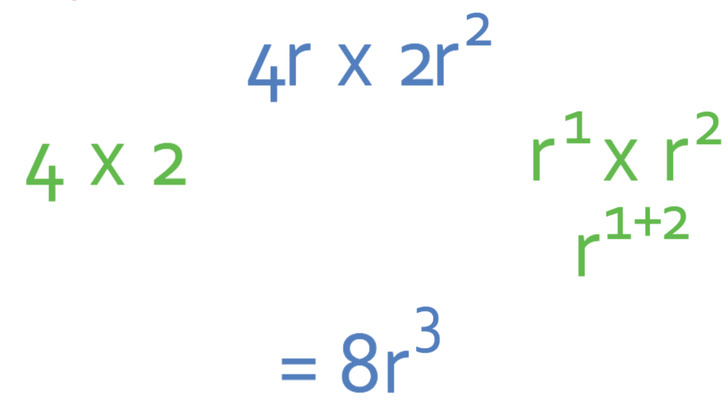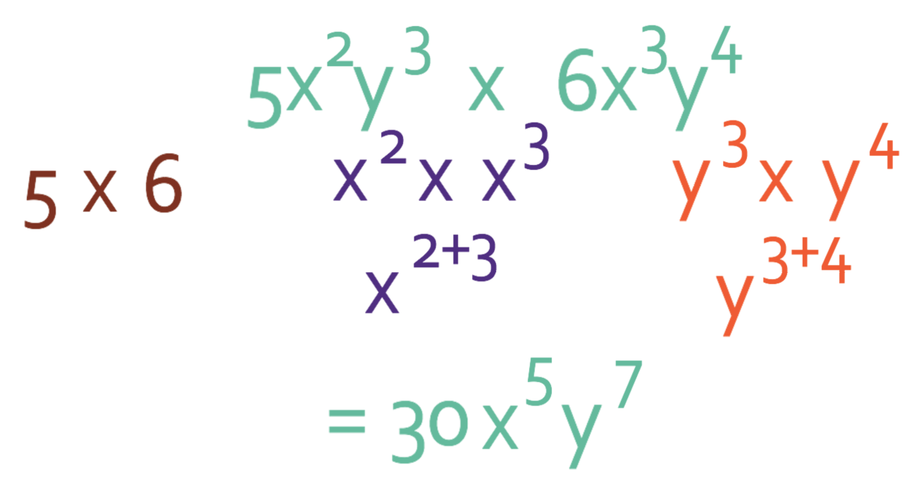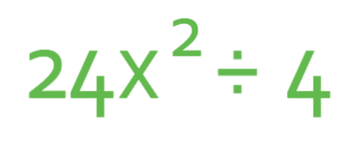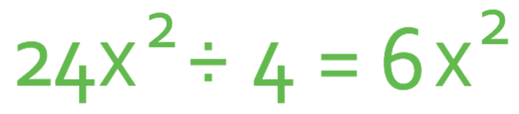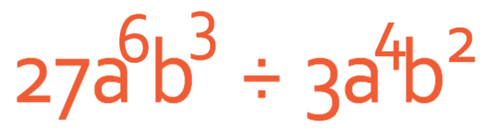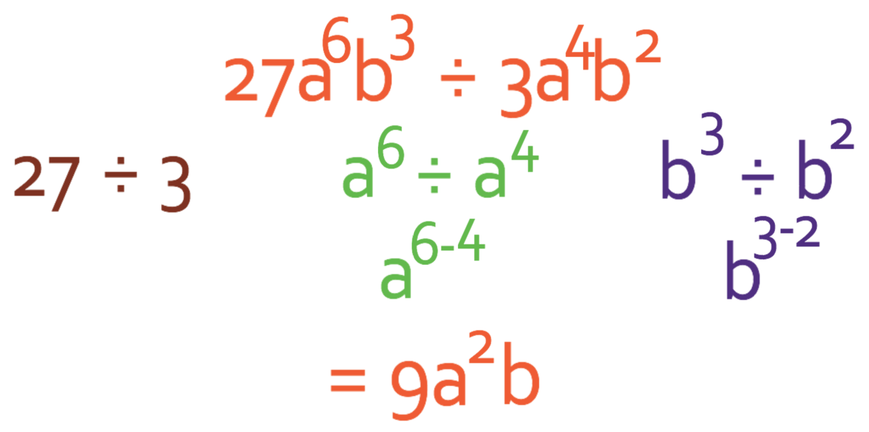2.1 C) Simplifying Expressions – Part 2
Simplifying by using letters and numbers is used when we are multiplying or dividing terms. Before you work through this section, you may find it useful to go through the indices and powers section (click here to be taken through to the indices and power section).
Example 1
Simplify the expression below.
This expression simplified is d2, which means d multiplied by itself.
Example 2
Simplify the expression below.
The best way to simplify this expression is to multiply the numbers together and then multiply out all of the different unknowns (there is only one unknown in this question (the unknown w), but often there will be more than 1 unknown – see example 4)
To find the number in the simplified answer, we multiply 3 by 4, which gives us 12. There are no w’s in the first term and a w is the second term, which means that there will be a w in the simplified answer. Therefore, the simplified expression is 12w.
Example 3
Simplify the expression below.
Like the question before, we will obtain the simplified answer by multiplying the numbers and then multiplying each of the unknowns (again there is only one unknown, the unknown r).
To obtain the number in the simplified answer, we multiply 4 by 2, which gives us 8.
We now multiply out the r’s. The first term has r and the second term has r2. Therefore, we are multiplying r x r2. These terms have the same base, which means that we add the powers. Therefore, we have r3 (r x r2 = r1 + 2 = r 3).
This means that the simplified answer is 8r3.
Example 4
Simplify the expression below.
We are going to use the same method as before. We are going to multiply the number and then each of the unknowns.
Let’s start with the numbers. We obtain the number in the simplified answer by multiplying 5 by 6, which gives us 30.
There are two different unknowns in this question; x and y. We simplify each one of these separately.
For the x’s, we are multiplying x2 by x3. As we are multiplying power with the same base, we add the powers, which gives us x5 (x2 x x3 = x2 + 3 = x5).
For the y’s, we are multiplying y3 by y4, which is y7 (y3 x y4 = y3+4 = y7).
The final step is to combine them all. This means that the answer is 30x5y7.
Dividing
We use exactly the same method for dividing; we just need to be a little bit careful with the rules to do with powers. When we are dividing powers that have the same base, we take away the powers.
Example 5
Simplify the expression below.
As with the multiplication examples, we divide the numbers and then each of the unknowns.
To obtain the number for the simplified answer, we divide 24 by 4, which is 6.
There are no unknowns on the number that we are dividing by, which means that the x2 goes through to the answer.
The simplified answer for this question is 6x2.
Example 6
Simplify the expression below.
We answer this question in the same way as all of the previous questions; we work with the numbers and then each of the unknowns.
For the numbers, we are dividing 27 by 3, which gives 9.
There are two different unknowns in this equation; a and b. When we are dividing powers with the same bases, we take the powers away from one another.
For the a’s; a6 ÷ a4 = a6 – 4 = a2
The b’s; b3 ÷ b2 = b3 – 2 = b1 = b
The final step is to combine all of these, which gives us the simplified answer as 9a2b.