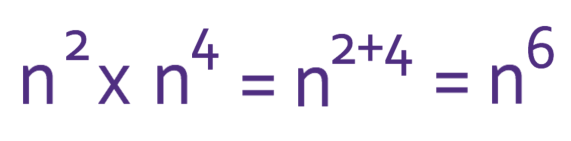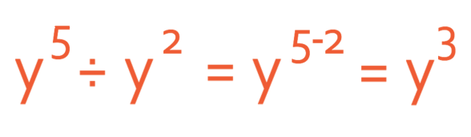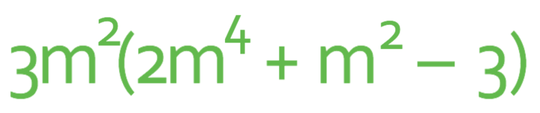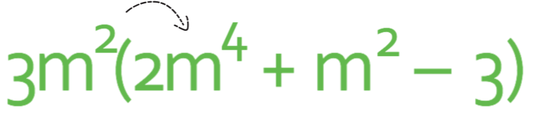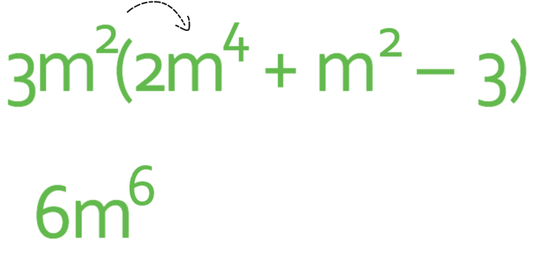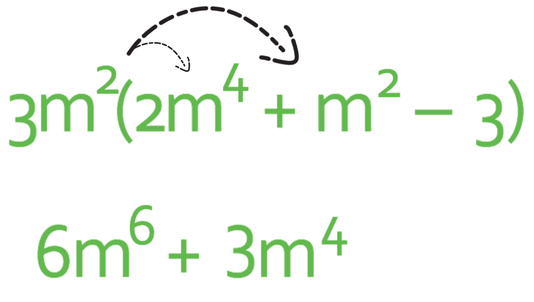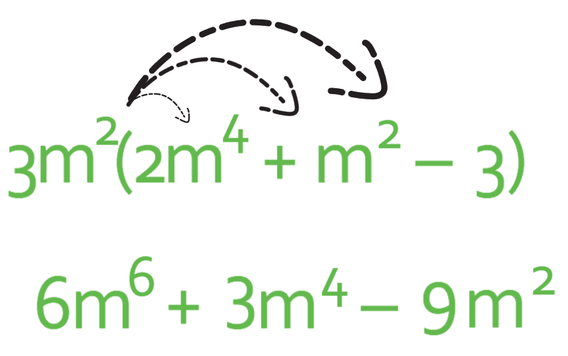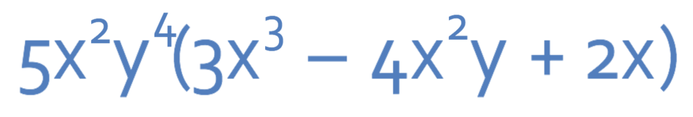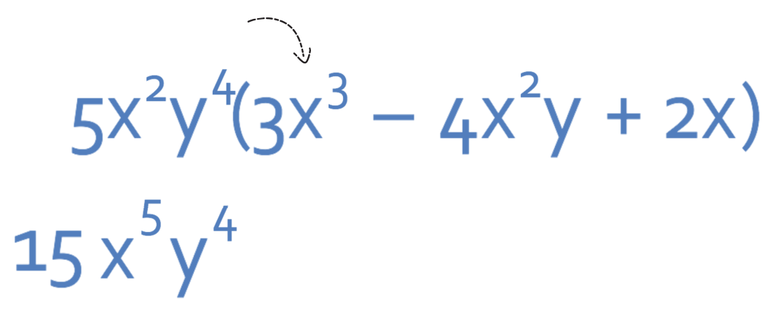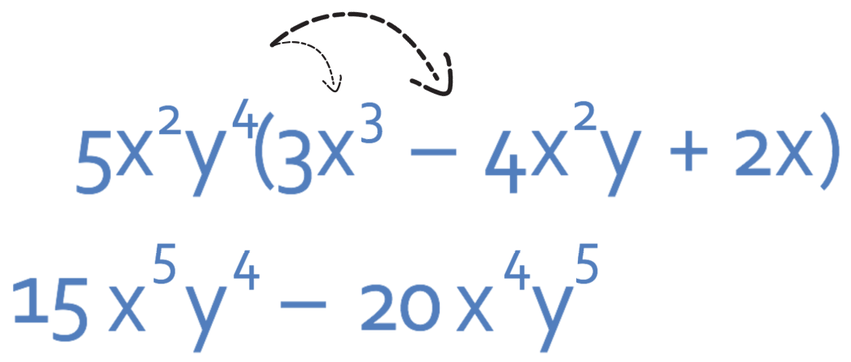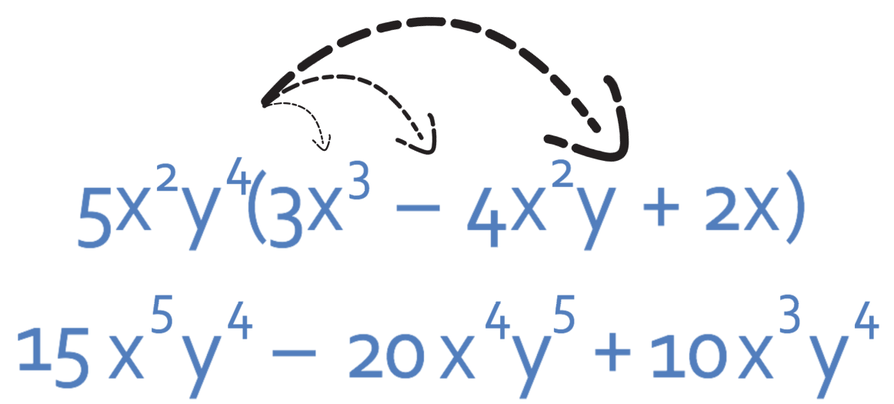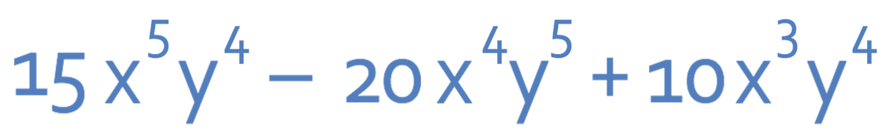2.1 F) Expanding Brackets with Powers
When we multiply indices that have the same base, we add the powers.
Also, when we are dividing indices that have the same bases, we take the powers from one another.
However, we need to make sure that the bases in the indices are the same because we are unable to combine them if they are not the same.
Example 1
Expand out the brackets below.
To expand out the bracket, we are going to be multiplying the term that is on the outside of the bracket (3m2) by each of the terms that are on the inside of the bracket. When we are multiplying the terms, it is best to multiply the signs, then the numbers and finally the unknowns.
I am going to use arrows to ensure that I multiply 3m2 by every term inside the bracket.
Let’s start with the first term.
For the first term, I am multiplying 3m2 by 2m4. Both of these terms are positive, which means that the answer will be positive. To obtain the number, I am multiplying 3 by 2, which is 6. Finally, we find the unknown by multiplying m2 by m4. Both of these indices have the same base of m, and we are multiplying them, which means that we add the powers together; m2 x m4 = m2+4 = m6. Therefore, the first term of the expanded expression is 6m6.
We do the same for the second term. To obtain the second term, we are multiplying 3m2 by m2. Both of these terms are positive, which means that the expanded term will be positive. We obtain the number by multiplying 3 by 1, which is 3. The final step is to multiply out the unknowns, which is m2 x m2. This gives us m4. We can now combine the outcomes of each of the steps to give us 3m4.
We are now on to multiplying 3m2 by the final term in the bracket (-3). We are multiplying a positive by a negative, which is going to give us a negative. To obtain the number, we are multiplying 3 by 3, which give us 9. Finally, we multiply the unknowns (the m’s). There are no unknowns in the term in the bracket, which means that we just get m2. Therefore, the final expanded term is -9m2
There are no common terms in the expression above, which means that the expression is in it’s simplest form.
Example 2
Expand out the brackets below.
We are going to use the same strategy as before; multiply the signs, multiply the numbers and finally multiply the unknowns. There are two unknowns in this question, so it is best to split multiplying the unknowns into two separate ones; i.e. multiply out the x’s and then multiply out the y’s.
Let’s start by multiplying 5x2y4 by the first term in the bracket (3x2). Both of these terms are positive, which means that the expanded term is going to be positive. We now multiply the numbers; 5 multiplied by 3, which gives 15. The next step is to multiply the x’s; x2 multiplied by x3, which is x5. Finally, we multiply the y’s. There are no y’s in the term inside the bracket, which means that we have y4. We can now combine all of these together, which means that the first term in the expanded bracket is 15x5y4.
We do the same with the second term in the bracket; 5x2y4 x (-4x2y). Multiplying a positive by a negative will give us a negative. 5 multiplied by 4 is 20. x2 multiplied by x2 is x4. y4 multiplied by y is y5. This means that the second term is -20x4y5.
We are now onto the final term, which is 5x2y4 multiplied by 2x. Both of these terms are positive, which means that the answer will be positive. 5 multiplied by 2 is 10. x2 multiplied by x is x3. There are no y’s in the final term in the bracket, which means that we will have y4. The final term in the bracket is 10x3y4.
There are no common terms in the expression above, which means that the answer is in its simplest form. The final answer is given below.