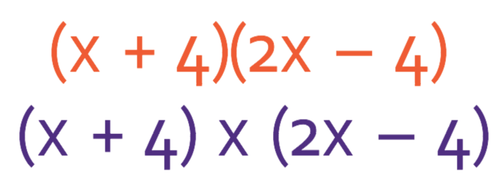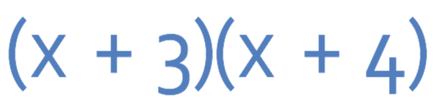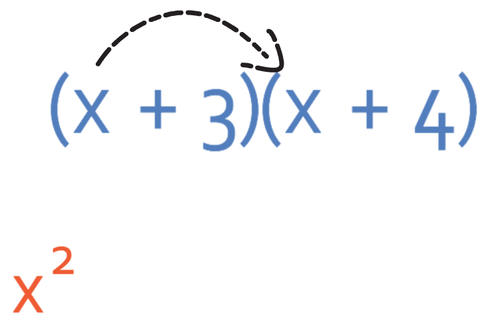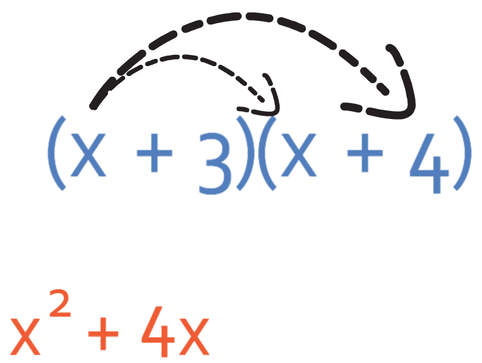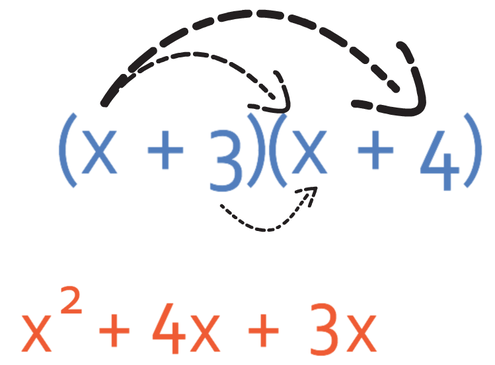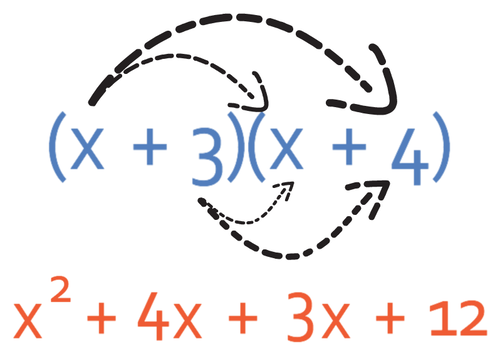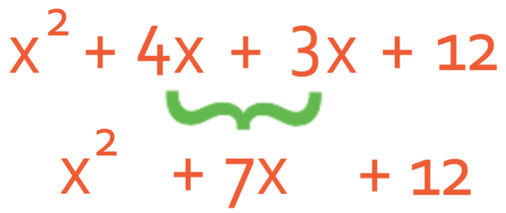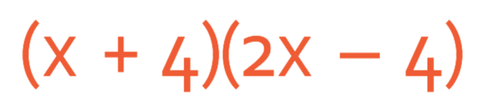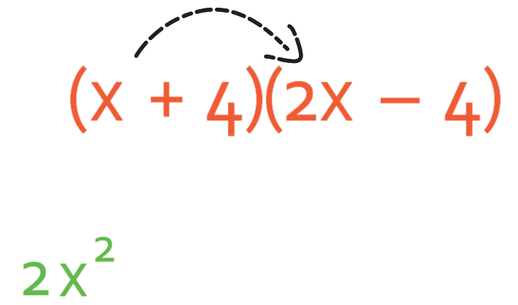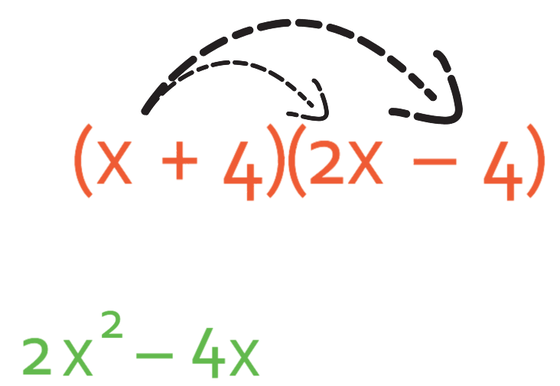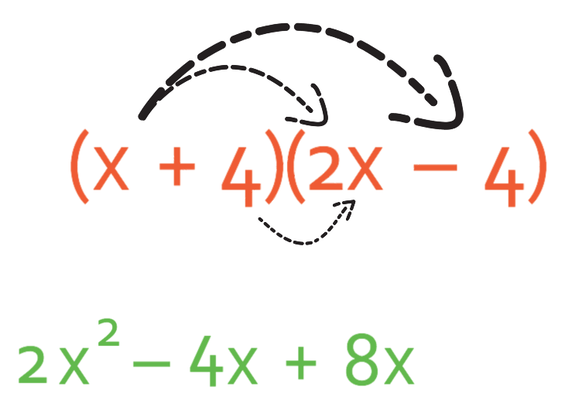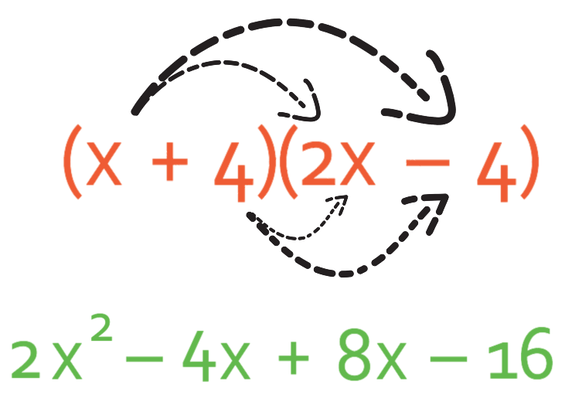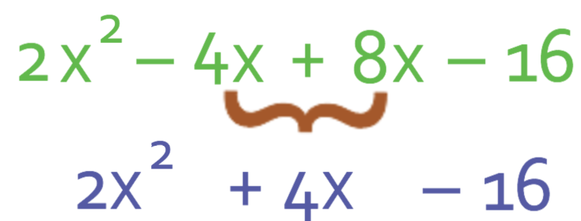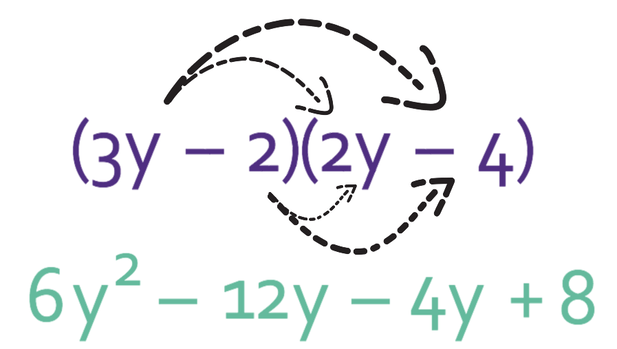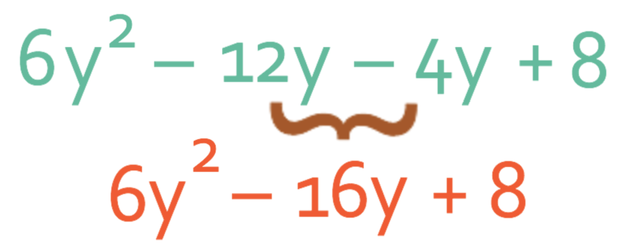Back to AQA Algebra Introduction (F) Home
2.1 H) Expanding Double Brackets – Part 1
​Two brackets next to each other means that the brackets are being multiplied together. For example:
​We can expand the brackets, which means multiplying out the brackets. When we expand, we multiply every term in the first bracket by every term in the second bracket. There are a few different ways that you are able to multiply out double brackets with two terms in each of the brackets. However, I think that it is best to stick with the method that works best for you. The one that works best for me is FOIL, which stands for First, Outside, Inside and Last. Also, when you are multiplying out the brackets, you may find it useful to include arrows to show what you are multiplying together.
Example 1

Expand the brackets below.

I am going to use the FOIL method (First, Outside, Inside and Last) to expand these double brackets. The first step in the FOIL method is to multiply the first term in each of the brackets together; we therefore multiply x by x, which gives us x2.

The next step in the FOIL method is to multiply the outside terms, which means that we multiply x and 4, which gives us 4x.

We are now onto the I in FOIL, which stands for inside. This means that we multiply 3 and x, which gives 3x.

We are now onto the last part of FOIL, which is the L and this stands for the last terms. This means that we are multiplying 3 by 4, which gives us 12.

The final step is to simplify and collect any like terms. There are 3 different types of terms in this expression; these different terms are x2, x and numbers. There are two different terms in the expression that contain x’s (4x and 3x). We are able to combine these two terms to give us 7x. This results in the expression becoming:

The FOIL method is a good way to ensure that we multiply out double brackets correctly.

Example 2
Let’s multiply out the brackets below. 

I am going to be using the FOIL method (First, Outside, Inside and Last). This means that I will be multiplying out the first terms in each of the two brackets, which is x and 2x. When we are multiplying out these two terms, you may find it easier to split it up into the signs, numbers and then unknowns (only x’s in this case). Both of the terms that we are multiplying are positive, which means that the answer will be positive. We now multiply the numbers; 1 multiplied by 2, which is 2. Finally, we multiply the x’s; x multiplied by x is x2. Therefore, the first term is 2x2.

​We now multiply the outside of the brackets, which is x from the first bracket and -4 from the second bracket. We are multiplying a positive by a negative, which will give us a negative. For the numbers, we are multiplying 1 by 4, which is 4. And there is one x. All of this together means that the outside terms multiplied together is -4x. 
​We are now onto the inside terms in the bracket, which is 4 multiplied by 2x. Both of these terms are positive, thus means that the answer will be positive. We are then multiplying 4 by 2, which gives us 8. Finally, there is an x from the second bracket. All of this together results in the inner terms multiplied together being 8x. 
Finally, we multiply the last two terms in the brackets, which is 4 multiplied by -4. There is one positive and one negative, which results in the answer being negative. We are then multiplying 4 by 4, which is 16. Therefore, the last term is -16.

We now need to make sure that we have simplified the answer. There is only one term that has x2 in it and one term that only has numbers in it. However, there are two terms that contain x in and we can combine these terms. When we are combining the terms, we need to be careful about the signs that come before the terms. The two terms that we are combining are -4x and 8x, which when combined is 4x (-4x + 8x = 4x). The simplified expression is:

Example 3
Expand and simplify the bracket below.

Like the question before, I am going to use the FOIL method.

 

We multiple the First terms first: 3y x 2y = 6y2

 

Next, we multiply the terms on the Outside of the brackets: 3y x (-4) = -12y

 

Wen then multiply the terms on the Inside of the brackets: (-2) x 2y = -4y

 

Finally, we multiply the Last terms in each of the brackets: (-2) x (-4) = 8

 

We combine all of these values to give us:

The final step is to make sure that we have simplified our answer, which we do by collecting the two terms that have just y in; we can collect -12y and -4y together, which results in -16y. This results in the expression becoming.