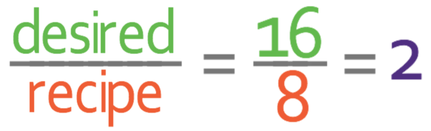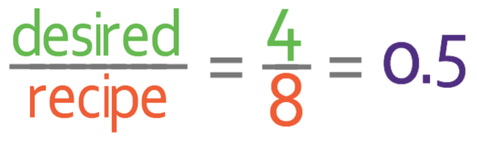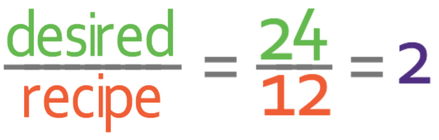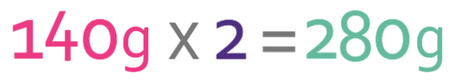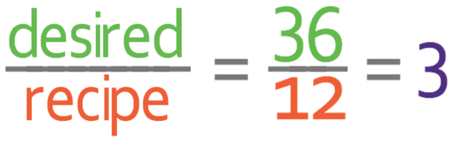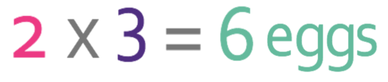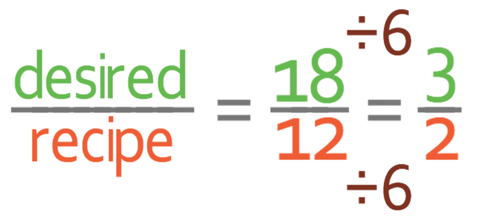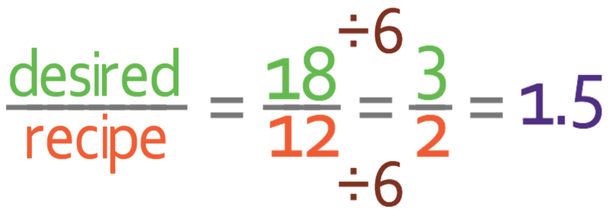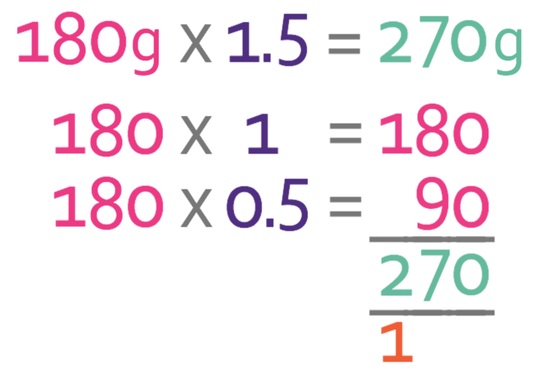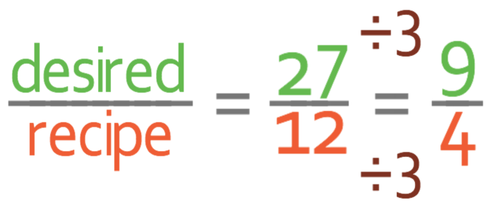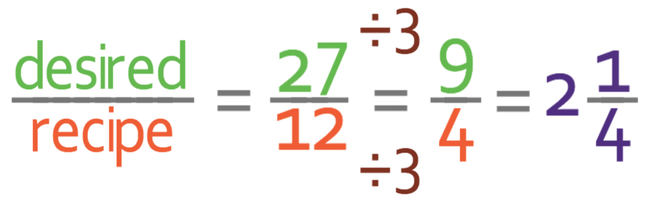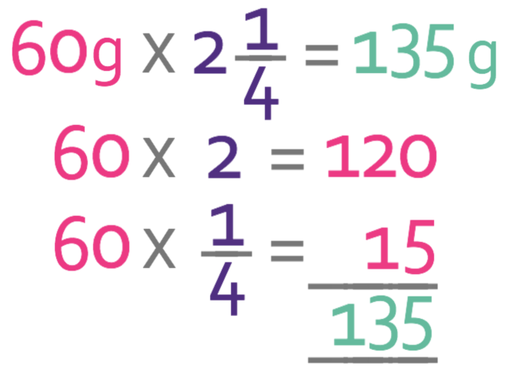Back to AQA Direct & Inverse Proportion (F) Home
3.1 A) Recipe Questions – Part 1
3.1 A) Recipe Questions – Part 1
The mass of the ingredients to make a cake is in direct proportion to the number of cakes that we are making. Direct proportion means that the variables move in the same direction and by the same proportion. The more cakes that we make, the greater the mass of the different ingredients needed to make the cake. The fewer cakes that we make, the lower the mass of the different ingredients needed to make the cake.
We are now going to have a few examples whereby we are given a recipe for a certain number of cakes (or other baked goods) and asked to find the quantities of the different ingredients if a different number of cakes are made.
We are now going to have a few examples whereby we are given a recipe for a certain number of cakes (or other baked goods) and asked to find the quantities of the different ingredients if a different number of cakes are made.
Example 1
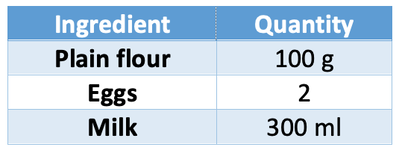
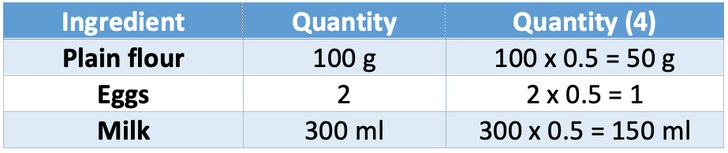
The table below shows the ingredients required to make 8 pancakes.
The table below shows the ingredients required to make 8 pancakes.
Answer the following questions:
a) What quantity of the ingredients would be required to make 16 pancakes?
b) What quantity of the ingredients would be required to make 4 pancakes?
Do not use a calculator for any of these questions.
Part a
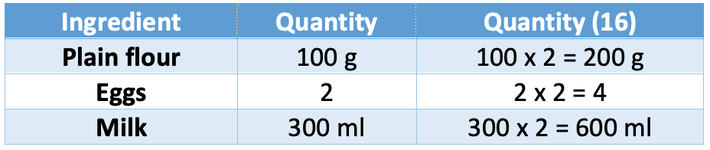
This part asks us to work out the quantities of ingredients required to make 16 pancakes. The recipe is for 8 pancakes and we want to make 16 pancakes. Therefore, we can make 16 pancakes by doubling the ingredients. The working is shown in the table below:
a) What quantity of the ingredients would be required to make 16 pancakes?
b) What quantity of the ingredients would be required to make 4 pancakes?
Do not use a calculator for any of these questions.
Part a
This part asks us to work out the quantities of ingredients required to make 16 pancakes. The recipe is for 8 pancakes and we want to make 16 pancakes. Therefore, we can make 16 pancakes by doubling the ingredients. The working is shown in the table below:
For this question, it was quite easy to see what we needed to multiply the recipe by. However, if we were unsure about what we needed to multiply the different ingredients by, we can divide the desired quantity (16) by the quantity that the recipe is for (8). The working is shown below:
This tells us that we need to multiply all of the ingredients by 2 in order to make 16 pancakes.
Part b
Part b asks us to make 4 pancakes. We work out what we need to multiply the recipe by to make 4 pancakes by dividing the desired quantity of pancakes (4) by the number of pancakes that the recipe is for (8).
Part b
Part b asks us to make 4 pancakes. We work out what we need to multiply the recipe by to make 4 pancakes by dividing the desired quantity of pancakes (4) by the number of pancakes that the recipe is for (8).
This tells us that we need to multiply the ingredients in the recipe by 0.5; multiplying by 0.5 is the same as halving. The working is shown in the table below.
Example 2
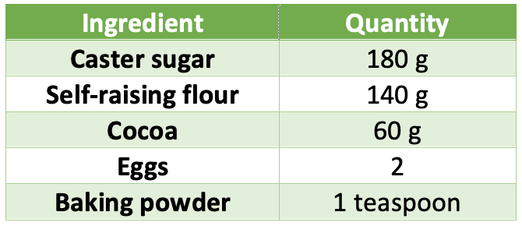
Here are the ingredients required to make 12 chocolate cupcakes.
Here are the ingredients required to make 12 chocolate cupcakes.
Answer the following questions:
a) What quantity of self-raising flour is needed to make 24 chocolate cupcakes?
b) How many eggs are needed to make 36 chocolate cupcakes?
c) What quantity of sugar is needed to make 18 chocolate cupcakes?
d) What quantity of cocoa is required to make 27 chocolate cupcakes?
Do not use a calculator for any of these questions.
Part a
The recipe that we are given in the question makes 12 cupcakes. Part a asks us to make 24 cupcakes. We are able to work out what we need to multiply the recipe by to make 24 cupcakes by dividing the desired number of cupcakes (24) by the number of cupcakes that the recipe is for (12).
a) What quantity of self-raising flour is needed to make 24 chocolate cupcakes?
b) How many eggs are needed to make 36 chocolate cupcakes?
c) What quantity of sugar is needed to make 18 chocolate cupcakes?
d) What quantity of cocoa is required to make 27 chocolate cupcakes?
Do not use a calculator for any of these questions.
Part a
The recipe that we are given in the question makes 12 cupcakes. Part a asks us to make 24 cupcakes. We are able to work out what we need to multiply the recipe by to make 24 cupcakes by dividing the desired number of cupcakes (24) by the number of cupcakes that the recipe is for (12).
Therefore, we need to multiple the recipe by 2 (we double the recipe). We are only asked to find the quantity of self-raising flour, so we just multiply 140g by 2.
This tells us that we need 280 g of self-raising flour.
Part b
Part b asks us to find the number of eggs required to make 36 cupcakes. We find out what we need to multiply the recipe by to make 36 cupcakes by dividing the desired quantity (36) by the amount that the recipe is for (12).
Part b
Part b asks us to find the number of eggs required to make 36 cupcakes. We find out what we need to multiply the recipe by to make 36 cupcakes by dividing the desired quantity (36) by the amount that the recipe is for (12).
This tells us that we need to multiply the recipe by 3. We are only asked to find the number of eggs required. 2 eggs are required to make 12 cupcakes, so we find the number of eggs needed to make 36 cupcakes by multiply 2 by 3.
We need 6 eggs to make 36 cupcakes.
Part c
This part asks us to find the quantity of sugar needed to make 18 cupcakes. We find out what we need to multiply the recipe by to make 18 cupcakes by dividing the desired quantity (18) by the amount that the recipe makes (12).
Part c
This part asks us to find the quantity of sugar needed to make 18 cupcakes. We find out what we need to multiply the recipe by to make 18 cupcakes by dividing the desired quantity (18) by the amount that the recipe makes (12).
I am going to simplify the fraction, so that it is slightly easier to work with. We simplify the fraction by looking for common factors between the numerator (18) and the denominator (12). 6 is a common factor, so we can divide both the numerator and the denominator by 6.
3/2 is the same as 1.5.
Therefore, in order to make 18 cupcakes, we need to multiply the recipe by 1.5. We want to know the quantity of sugar, so we multiply the current quantity of sugar (180 g) by 1.5.
The easiest way to multiply by 1.5 is to multiply by 1 and then by 0.5 (a half). We then add the outcomes.
This tells us that we need 270 g of sugar to make 18 cupcakes.
Part d
This part asks us to find the quantity of cocoa needed to make 27 cupcakes. We find out what we need to multiply the recipe by to make 27 cupcakes by dividing the desired quantity (27) by the amount that the recipe makes (12). I am going to have this number as a fraction.
Part d
This part asks us to find the quantity of cocoa needed to make 27 cupcakes. We find out what we need to multiply the recipe by to make 27 cupcakes by dividing the desired quantity (27) by the amount that the recipe makes (12). I am going to have this number as a fraction.
I am now going to simplify the fraction and then convert it from an improper fraction to a mixed number (the fraction is improper because the numerator is larger than the denominator). Both 27 and 12 are multiplies of 3. Therefore, I am going to divide the numerator and denominator of the fraction by 3.
We convert this improper fraction into a mixed number by dividing the numerator (9) by the denominator (4). When we do this, we see that 4 goes into 9 twice with a remainder of 1 (the number of times that the denominator fully goes into the numerator will be the number part of the mixed number; the number part will be 2. And, the remainder will be the numerator for the fraction part of the mixed number; the numerator of the fraction part will be 1. The denominator of the fraction part of the mixed number will stay the same; it will be 4). This means that 9/4 as a mixed number is 2 ¼.
Therefore, we can find the quantities of the different ingredients needed to make 27 cupcakes by multiplying the recipe by 2 ¼. We only want to know the quantity of cocoa, so we multiply the current quantity of cocoa (60 g) by 2 ¼.
The easiest way to do this is to multiply by 2 and then by ¼ (which we can do by dividing by 4, or by halving and halving again). We then add the outcomes. The working is shown below.
This tells us that we need 135 g of cocoa.