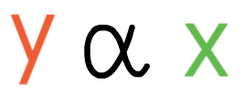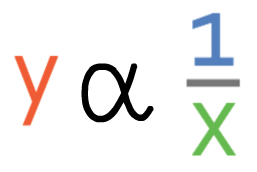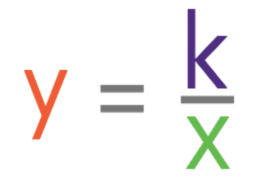Back to AQA Direct & Inverse Proportion (F) Home
3.1 D) Direct & Inverse Proportion Notation and Equation
3.1 D) Direct & Inverse Proportion Notation and Equation
Direct Proportion
From the previous sections, we learnt that variables that are in direct proportion move in the same direction as one another and by the same proportion. For example, if we had two variables that are in direct proportion (variable x and variable y), and variable x was to triple, variable y would also triple. Also, if variable x was to halve, variable y would also halve.
The notation for variables x and y being in direct proportion is:
From the previous sections, we learnt that variables that are in direct proportion move in the same direction as one another and by the same proportion. For example, if we had two variables that are in direct proportion (variable x and variable y), and variable x was to triple, variable y would also triple. Also, if variable x was to halve, variable y would also halve.
The notation for variables x and y being in direct proportion is:
With the general equation:
k in the above equation is a constant (a number).
Inverse Proportion
Variables that are inversely proportional to each other move in opposite directions. If one variable increases, the other variable decreases. If one variable decreases, the other variable increases.
An example would be the number of road workers and the time taken to resurface a road. The more road workers there are, the less time it takes to resurface the road. The fewer road workers there are, the more time that it takes to resurface the road.
Another example would be the average speed of a runner and the time taken to finish a race. The higher the average speed of the runner, the less time it takes to finish the race. The lower the average speed of the runner, the greater the time it takes to finish the race.
If y was inversely proportional to x, the notation would be:
Variables that are inversely proportional to each other move in opposite directions. If one variable increases, the other variable decreases. If one variable decreases, the other variable increases.
An example would be the number of road workers and the time taken to resurface a road. The more road workers there are, the less time it takes to resurface the road. The fewer road workers there are, the more time that it takes to resurface the road.
Another example would be the average speed of a runner and the time taken to finish a race. The higher the average speed of the runner, the less time it takes to finish the race. The lower the average speed of the runner, the greater the time it takes to finish the race.
If y was inversely proportional to x, the notation would be:
With the general equation:
The value of the k in the general equation is a number.
End Note
It is worth getting the notation and general equation for direct and inverse proportion down on a revision card because they can be quite tricky to remember.
It is worth getting the notation and general equation for direct and inverse proportion down on a revision card because they can be quite tricky to remember.