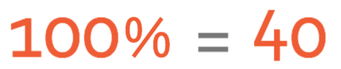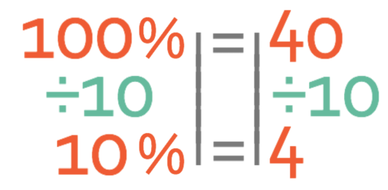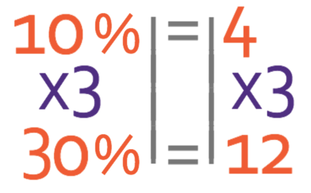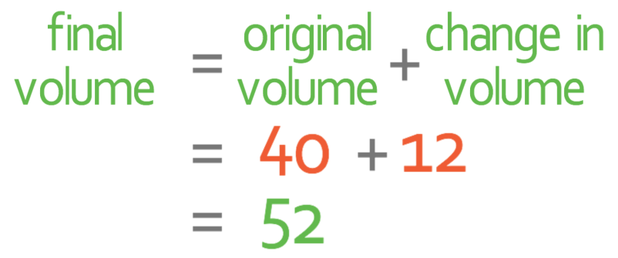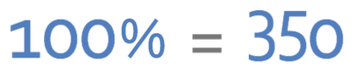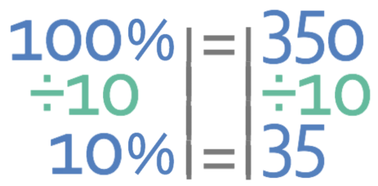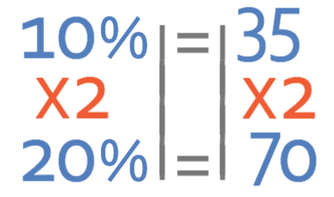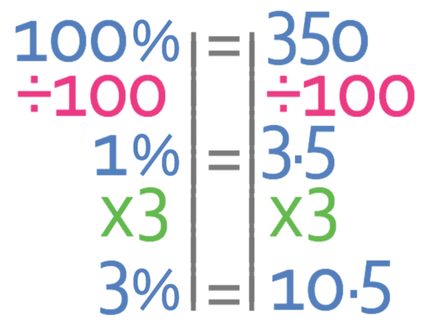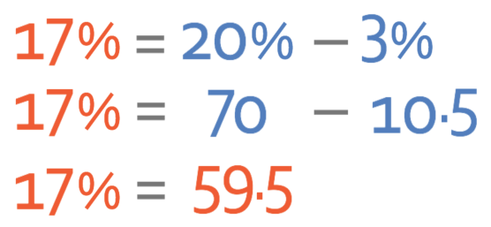Back to AQA Percentages (F) Home
3.2 G) Increasing or Decreasing by a Certain Percentage – Non-Calculator
3.2 G) Increasing or Decreasing by a Certain Percentage – Non-Calculator
This section and the next section will explore increasing or decreasing an amount by a certain percentage. In this section, we are going to be looking at the method that we use when we are not able to use a calculator. In the next section, we are going looking at the method that we use when we do have a calculator.
Non-Calculator
When we do not have access to a calculator, it is easier to find the percentage that we are adding on (or taking off) and then add it on (or take it off) from the original amount.
When we do not have access to a calculator, it is easier to find the percentage that we are adding on (or taking off) and then add it on (or take it off) from the original amount.
Example 1
For example, I place dough in the fridge to rise. The volume is currently 40 cubic centimetres. After 20 minutes the volume of the dough increases by 30%. What is the volume of the dough after 20 minutes?
The first step in answering this question is to work out what 30% of 40 cubic centimetres is. It is easier to find out what 10% of the dough is and then multiply by 3, which will give us what 30% is (10% x 3 = 30%).
The total amount of dough is 40 cubic centimetres, and this represents 100%. We can create the following equation from this information.
For example, I place dough in the fridge to rise. The volume is currently 40 cubic centimetres. After 20 minutes the volume of the dough increases by 30%. What is the volume of the dough after 20 minutes?
The first step in answering this question is to work out what 30% of 40 cubic centimetres is. It is easier to find out what 10% of the dough is and then multiply by 3, which will give us what 30% is (10% x 3 = 30%).
The total amount of dough is 40 cubic centimetres, and this represents 100%. We can create the following equation from this information.
The next step is to find out what 10% is, and we are able to do this by dividing both sides of the above equation by 10.
We want to find 30% and not 10%. Therefore, we need to multiply both sides of the equation by 3.
30% is 12 cubic centimetres and this is the change in volume of the dough. We are told that the volume of our dough increases by 30% (12 cubic centimetres), so we obtain our final answer by adding the change in the volume of the dough (12 cubic centimetres) to the original volume of the dough (40 cubic centimetres).
Therefore, the final volume of our dough is 52 cubic centimetres.
Example 2
I leave a glass that contains 350 ml of water in the sun for 20 minutes. During this time, 17% of the water evaporates. How much water is left in the container? Do not use a calculator.
We are not able to use a calculator for this question, so we need to find out what 17% of 350 ml of water is. Also, the water is evaporating away, which means that the amount of water in the cup is going to be decrease. Therefore, when we have found what 17% is, we will take it off the starting amount of water, which is 350 ml.
I think the best method to find 17% is to find 20% and take 3% off of 20%. Let’s start by finding what 20% of 350 ml is. The amount of water at the start (350 ml) represents 100%. This gives us the equation below.
I leave a glass that contains 350 ml of water in the sun for 20 minutes. During this time, 17% of the water evaporates. How much water is left in the container? Do not use a calculator.
We are not able to use a calculator for this question, so we need to find out what 17% of 350 ml of water is. Also, the water is evaporating away, which means that the amount of water in the cup is going to be decrease. Therefore, when we have found what 17% is, we will take it off the starting amount of water, which is 350 ml.
I think the best method to find 17% is to find 20% and take 3% off of 20%. Let’s start by finding what 20% of 350 ml is. The amount of water at the start (350 ml) represents 100%. This gives us the equation below.
The best way to find 20% is to find 10% and then multiply by 2. We find 10% by dividing both sides of the equation by 10.
We now need to multiply by 2 because we want to find out what 20% is and not 10%.
We have now found that 20% of 350 ml is 70 ml. The next step is to find out what 3% of 350 ml is and take what 3% is off the value of 20% of 350 ml (which was 70 ml). The best way to find what 3% of 350 ml is, is to divide 350 ml by 100 to obtain the value for 1% and then to multiply that value by 3 to obtain what 3% is.
We now know what 20% and 3% of 350 ml is and we can use both of these values to find out what 17% is by taking our value for 3% from the value for 20%.
Therefore, 17% is 59.5 ml and this is the amount of water that has evaporated (it is the amount of water that is lost). The final step to answer the question is to take the amount of water that evaporated from the original amount of water in the glass and this is because we were asked to find the amount of water left in the glass.
The glass has 290.5 ml left in it after it has been left in the sun.