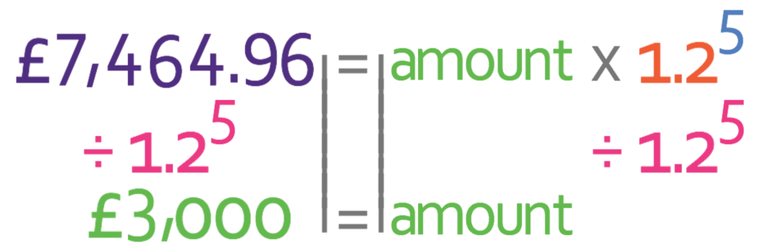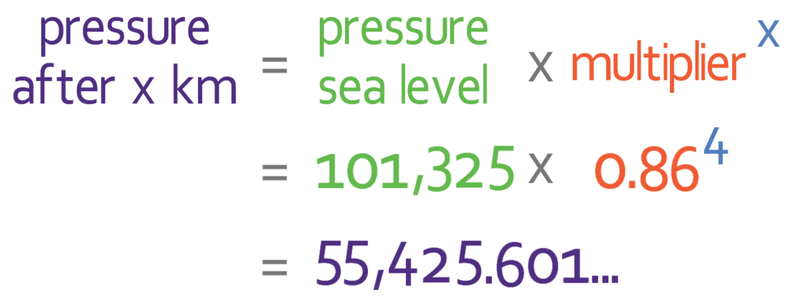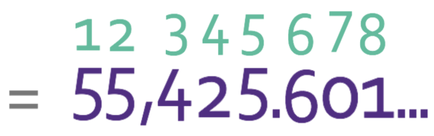In this section we are going to be looking at a few examples that are slightly different to the usual examples. The content in this section builds on the content that was discussed in the previous section. Before working through the content in this section, make sure that you have worked through the content in the previous two sections (click here to be taken to part 1 and click here to be taken to part 2).
Example 1
I place £5,000 into a bank account that receives a compound interest of 3.8% per year. Find the number of years that it will take me to earn at least £1,000 in interest.
This question asks us to find the number of years (the value of x) whereby the interest is at least £1,000. If I have earnt £1,000 interest, it will mean that the amount of the money in the bank account will be £6,000 because it will be the original £5,000 plus the £1,000 interest.
Therefore, we answer this question by subbing in values for x into the compound interest formula and we will be looking for the first value that gives an amount of money in the account that is £6,000 or above £6,000. We are looking for the lowest value of x where the inequality below works.
I place £5,000 into a bank account that receives a compound interest of 3.8% per year. Find the number of years that it will take me to earn at least £1,000 in interest.
This question asks us to find the number of years (the value of x) whereby the interest is at least £1,000. If I have earnt £1,000 interest, it will mean that the amount of the money in the bank account will be £6,000 because it will be the original £5,000 plus the £1,000 interest.
Therefore, we answer this question by subbing in values for x into the compound interest formula and we will be looking for the first value that gives an amount of money in the account that is £6,000 or above £6,000. We are looking for the lowest value of x where the inequality below works.
We are told in the question that the amount of money is £5,000. We can work the multiplier out by adding the interest (3.8%) onto 100% to give us 103.8% (100% + 3.8%). We then divide 103.8% by 100 to give us the multiplier of 1.038. The modified inequality becomes:
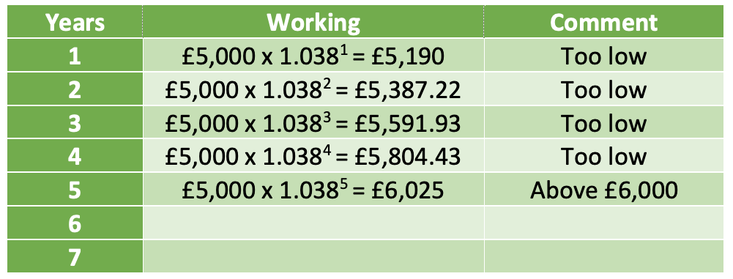
I am going to use the table below starting with the number of years as 1 (x as 1).
The first year where the amount of interest is £1,000 or more is year 5. Therefore, the answer to this question is 5 years.
Example 2
I place some money into a bank account for 5 years. The money in the bank receives a compound interest of 20% per year. The total amount of money after the 5 years is £7,464.96. How much money was originally in the bank account?
The best way to answer these types of questions is to start by getting the compound interest formula down.
I place some money into a bank account for 5 years. The money in the bank receives a compound interest of 20% per year. The total amount of money after the 5 years is £7,464.96. How much money was originally in the bank account?
The best way to answer these types of questions is to start by getting the compound interest formula down.
I am now going to place all of the values that we are given in the question into the formula. We are told in the question that the money was kept in the bank for 5 year, and this means that x is 5. We are also told the “amount of money after x/5 years” is £7,464.96. I am going to place these values into the formula.
The question tells us that the rate of compound interest is 20%. From this information, we can work out the multiplier by adding the interest (20%) onto 100% to give us 120%. We then divide 120% by 100 to give a multiplier of 1.2. I have added the multiplier into the formula.
We want to find the “amount” and not the amount multiplied by 1.25. Therefore, we need to divide both sides of the equation by 1.25.
The amount of money saved was £3,000.
Comparison of Simple & Compound interest
A common exam question gives you two individuals that are saving a certain amount. These individuals will put their money into different bank accounts; one individual will have a bank account that pays simple interest and the other will have a bank account that pays compound interest. You will then be asked to work out who earns the most interest or the difference in the amount of interest earnt. We answer questions like this by working out the amount of money that each individual has in their bank account. Then, we compare the amounts in the bank accounts to see who has earnt the most interest. I am not going to go through an example like this, but there are a few questions like this in the quiz.
A common exam question gives you two individuals that are saving a certain amount. These individuals will put their money into different bank accounts; one individual will have a bank account that pays simple interest and the other will have a bank account that pays compound interest. You will then be asked to work out who earns the most interest or the difference in the amount of interest earnt. We answer questions like this by working out the amount of money that each individual has in their bank account. Then, we compare the amounts in the bank accounts to see who has earnt the most interest. I am not going to go through an example like this, but there are a few questions like this in the quiz.
Example 3
Sometimes it will be the case that we will be answering questions using something very similar to the compound interest formula. This is an example from a past paper question:
The pressure at sea level is 101,325 pascals.
Any rise of 1 km above sea level decreases the pressure by 14%.
For example,
Sometimes it will be the case that we will be answering questions using something very similar to the compound interest formula. This is an example from a past paper question:
The pressure at sea level is 101,325 pascals.
Any rise of 1 km above sea level decreases the pressure by 14%.
For example,
At 3km above sea level the pressure is 14% less than at 2km
Work out the pressure at 4 km above sea level.
Give your answer to 2 significant figures.
The question tells us that for every km that we rise above sea level the pressure decreases by 14%. This means that this question is very similar to a compound interest question (it is very similar to a compound interest question because with compound interest, the amount of money in the account between years increases by the same percentage. For example, if we had a compound interest of 6%, the increase in money between any consecutive years (such as year 3 to year 4) will be 6%). Therefore, I am going to start answering this question by writing down the compound interest formula:
Give your answer to 2 significant figures.
The question tells us that for every km that we rise above sea level the pressure decreases by 14%. This means that this question is very similar to a compound interest question (it is very similar to a compound interest question because with compound interest, the amount of money in the account between years increases by the same percentage. For example, if we had a compound interest of 6%, the increase in money between any consecutive years (such as year 3 to year 4) will be 6%). Therefore, I am going to start answering this question by writing down the compound interest formula:
I am now going to modify this formula so that it works for the question that we are answering. We are told the pressure at sea level (101,325 pascals) and we are told that the pressure decreases by 14% per 1 km rise above sea level. Therefore, the value of x will be the number of kilometres (km) above sea level. The modified formula is:
The question tells us the pressure at sea level is 101,325 pascals. Also, we are asked to find the pressure at 4 km above sea level, which means that x is 4. The question tells us that for every rise of 1 km, the pressure decreases by 14% and from this information, we can work out the multiplier. As the pressure decreases, we take 14% off of 100%.
We convert this into a multiplier by dividing by 100.
The multiplier is 0.86.
We now have everything we need to use the formula; the pressure is 101,325, the multiplier is 0.86 and the number of km above sea level (x) is 4. We sub these values into the formula:
We now have everything we need to use the formula; the pressure is 101,325, the multiplier is 0.86 and the number of km above sea level (x) is 4. We sub these values into the formula:
The question asks us to round our answer to 2 significant figures. With significant figures, we start counting from the first non-zero on the left. This means that the first significant figure is 5, the second significant figure is 5, the third significant figure is 4 etc.
We are rounding to two significant figures, so we draw a line after the second most significant figure. We then look at the third most significant figure, which is a 4. 4 is less than 5, which means that we round down; the second most significant figure stays as a 5. We then replace all of the figures after the second most significant figure with a 0.
The pressure to 2 significant figures is 55,000 pascals.