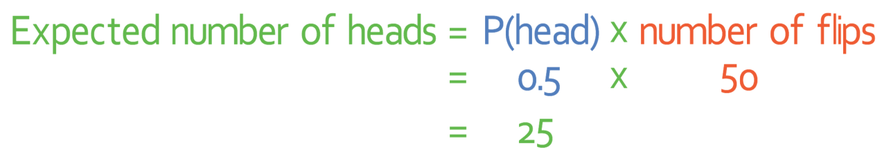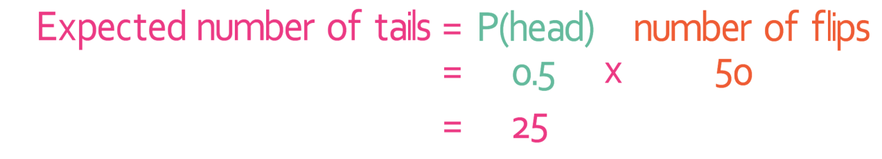5 G) Theoretical Probability & Relative Frequency
Let’s have an example of flipping a coin and we are going to flip a coin 50 times.
The probability of the coin landing on a head when flipped is 0.5 and we are flipping a coin 50 times. From this information, we are able to work out the expected number of times that the coin should land on a head. We do this by using by multiplying the theoretical probability of the coin landing on a head by the number of times that the coin is flipped.
We can do the same for the expect number of times that the coin will land on tails.
For example, I flipped a coin 50 times and there were 23 heads and 27 tails. These values are known as relative frequencies. These relative frequencies are different to the expected number of heads and tails that were predicted from the theoretical probabilities.
We are able to work out the probability of an event occurring from the relative frequencies.
Let’s work out the probability of obtaining a head from our relative frequencies. When we flipped a coin 50 times, the coin landed on heads 23 times, which means that the probability of obtaining heads when calculated from the relative frequencies is 23/50.
Let’s also work out the probability of the coin landing on tails from the relative frequencies. The coin was flipped 50 times and the coin landed on tails 27 times. This means that the probability of the coin landing on tails according to the relative frequencies is 27/50.
It may be case in the exam that you are asked to whether you think the coin (or dice or spinner) is fair. We answer questions like this by comparing the theoretical probability to the probability obtained from the relative frequencies. If the probabilities are quite close to one another, we would say that the coin (or dice or spinner) is fair. If the probabilities are quite far away from one another, you would say that the coin (or dice or spinner) is not fair.
For our example, the theoretical probability that a coin lands on a head is 0.5 and the probability from the relative frequency is 23/50, which when converted into a decimal is 0.46. 0.46 and 0.5 are very close to one another and this would imply that the coin that I flipped is fair.
We are able to increase the reliability of probabilities obtained from relative frequencies by increasing the number of times that we carry out our experiment (e.g. flipping a coin).
A common exam question will give you 3 individuals and ask you who has the best estimate for the probability. When they are asking for the “best”, they are referring to the most reliable and not the highest probability. The most reliable probability will be the one that has flipped the coin the greatest number of times.
Example
3 individuals flip a coin a certain number of times to obtain an estimate for the probability of obtaining a head. Who has the best estimate for the probability of obtaining a head?
We are able to work out who has the best estimate by working out who flipped the coin the greatest number of times. We work out the number of flips by adding up the number of heads and the number of tails for each of the friends. When we do this, we see that John flips the coin 20 times (14 + 6), Freya flips the coin 130 times (76 + 54) and Masie flips the coin 90 times (43 + 47). Freya flips the coin the greatest number of times and this means that her estimate for the probability of obtaining a head is the best (her estimate for obtaining a head is 76/130, which when simplified becomes 38/65).