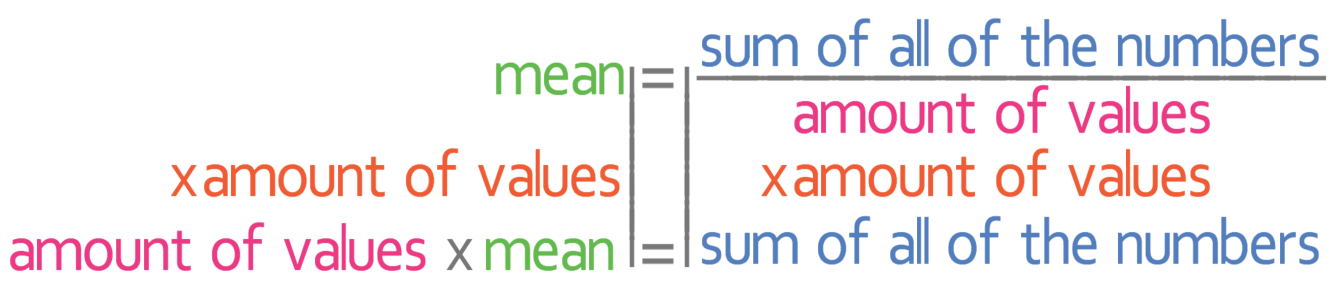
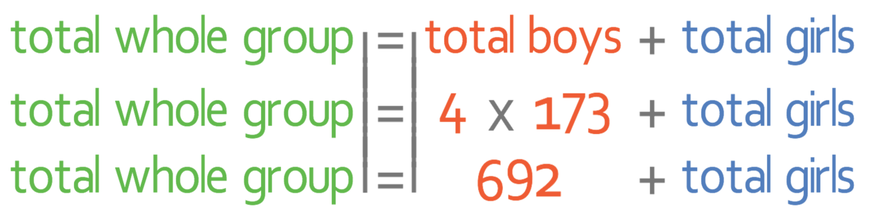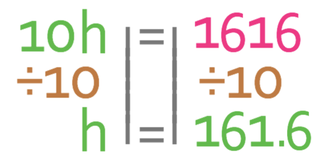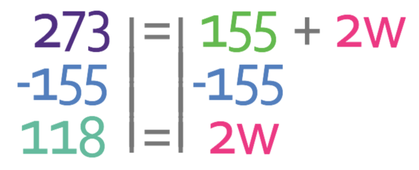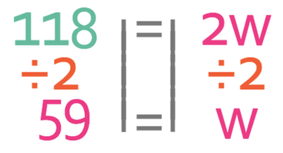In this section we are going to have a look at a few questions where we are given the mean and asked to work backwards. Before we have a look at some questions, it is best to remind ourselves of the mean formula, which is given below:
In the two examples in this section, we are going to be working out the “sums of all of the numbers”. We are able to find the “sum of all of the numbers” by multiplying both sides of the above formula by the “amount of values” (the denominator on the right side of the equation).
I will refer to the “sum of all of the numbers” as the totals for the rest of this section.
Example 1
A group of friends consists of 4 boys and 6 girls. The mean height of the boys is 173 cm and the mean height of the girls is 154 cm. What is the mean height of the whole group (boys and girls together)?
We answer questions like this by creating an equation whereby the total height for the group as a whole is equal to the total height of the group when split into different sub-groups. We get the equation:
A group of friends consists of 4 boys and 6 girls. The mean height of the boys is 173 cm and the mean height of the girls is 154 cm. What is the mean height of the whole group (boys and girls together)?
We answer questions like this by creating an equation whereby the total height for the group as a whole is equal to the total height of the group when split into different sub-groups. We get the equation:
We work out the total height by multiplying the number of individuals by the mean for their particular group (which is the second equation at the top). Let’s have a look at the total height of the boys first. We are told in the question that there are 4 boys and the mean height of the 4 boys is 173 cm. This means that we can work out the total height of the boys by multiplying 4 (the number of boys) by 173 cm (the mean height of the boys).
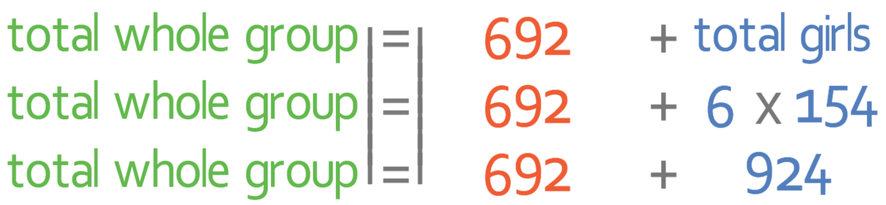
We can do the same to work out the total height for the girls. We are told in the question that there are 6 girls and the mean height of the girls is 154 cm. Therefore, we can work out the total height of the girls by multiplying 6 by 154.
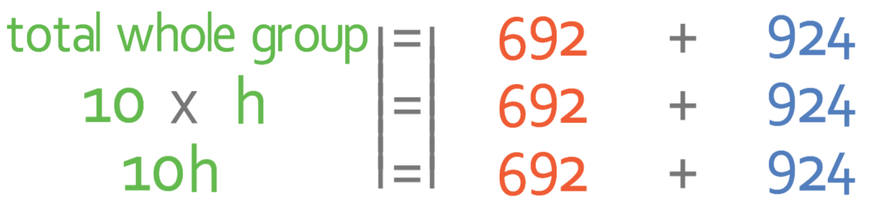
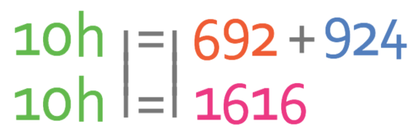
We now need to work with the left side of the equation, which is the total height for the whole group. We work out the total height for the whole group by multiplying the number of individuals in the whole group by the mean height for the whole group. We know that there are 10 individuals in the whole group (4 boys and 6 girls), but we do not know what the mean height is for the whole group. The mean for the whole group is what we are aiming to find out and I am going to let this be h. We can now work out what the total height for the whole group is by multiplying 10 (the number of individuals in the whole group) by h (the mean height for the individuals in the whole group).
It is now a case of solving this equation. The first step in solving this equation is to simplify the terms.
We want to find out what the value of h is and not 10h. Therefore, we divide both sides of the equation by 10.
This tells us that the mean height for the whole group is 161.6 cm. The final step for a question like this is to check whether the answer looks correct. We are told in the question that the mean height of the boys is 173 cm and the mean height of the girls is 154 cm. From this information, we would expect the mean height of the whole group to be somewhere in between these two values. The mean that we obtained was 161.6 cm, and this value is in between 173 cm and 154 cm, thus implying that we have got the correct answer. If you would have obtained a value for the means that was something like 184 cm, which is not in between 173 cm and 154 cm, you would be able to tell that you have obtained the wrong answer, which would allow you to recheck your workings and hopefully you will be able to find out where you have gone wrong. It is always a good idea to check your answer wherever possible.
Example 2
A clothing shop is open 7 days a week. The mean number of T shirts that they sell per day for the whole week is 39. The mean number of T shirts that they sell per day on a Monday to a Friday is 31. What is the mean number of T shirts that they sell per day on a weekend?
We start answering this question in exactly the same way that we answered the previous question; we create an equation whereby the total number of T shirts sold for the whole week (Monday to Sunday) is equal to the total number of T shirts sold for the different sub groups (the different sub groups for this question are Monday to Friday and weekends). The equation that we create is shown below:
A clothing shop is open 7 days a week. The mean number of T shirts that they sell per day for the whole week is 39. The mean number of T shirts that they sell per day on a Monday to a Friday is 31. What is the mean number of T shirts that they sell per day on a weekend?
We start answering this question in exactly the same way that we answered the previous question; we create an equation whereby the total number of T shirts sold for the whole week (Monday to Sunday) is equal to the total number of T shirts sold for the different sub groups (the different sub groups for this question are Monday to Friday and weekends). The equation that we create is shown below:
Let’s start by working out the total number of T shirts sold for the whole week. We are told in the question that the mean number of T shirts sold per day for the whole week is 39. Also, we know that there are 7 days in a week. Therefore, we can work out the total number of T shirts sold for the whole week by multiplying 7 by 39.
We can do the same for the total number of T shirts sold between Monday and Friday. We are told in the question that the mean number of T shirts sold per day between Monday and Friday is 31. We also know that there are 5 days between Monday and Friday. Therefore, we are able to work out the total number of T shirts sold between Monday and Friday by multiplying 5 by 31.
We now move onto the total number of T shirts sold at the weekend. We do not know what the mean number of T shirts sold per day at the weekend is and I am going to let the mean number of T shirts sold per day at the weekend equal w. There are 2 days at the weekend. Therefore, we can work out the total number of T shirts sold at the weekend by multiplying 2 by w.
We now need to solve the equation. We find the value of w by getting all of the terms that contain w to one side of the equation and all of the other terms to the other side of the equation. We have positive 2w on the right side of the equation and as it is positive, it makes sense to have all of the w’s on the right and all of the numbers on the left. This means that we need to move the 155 that is currently on the right to the left. We are able to do this by doing the opposite; we take 155 from both sides of the equation.
We want to find the value of w and not 2w. Therefore, we divide both sides of the equation by 2.
The mean number of T shirts that were sold per day at the weekend is 59.