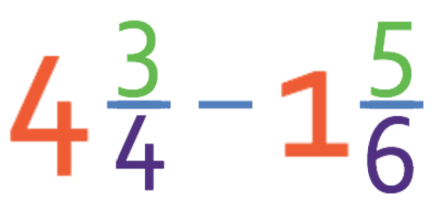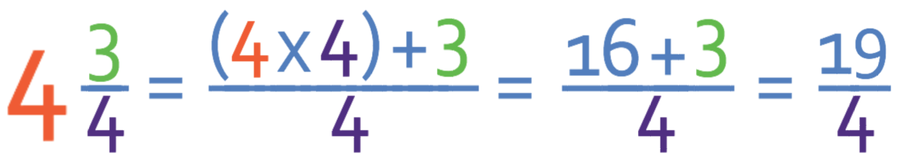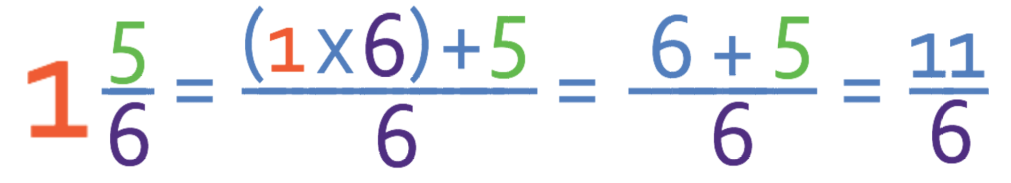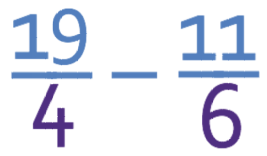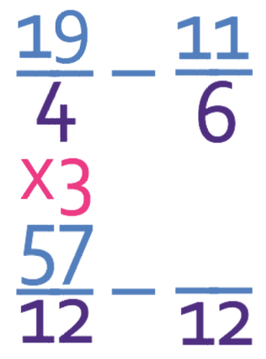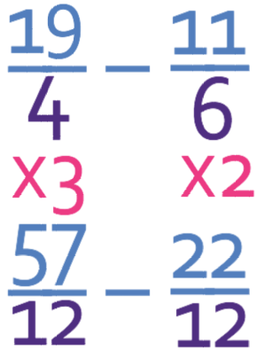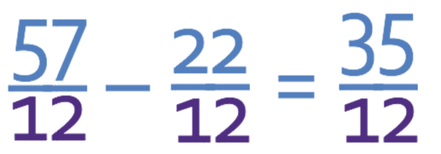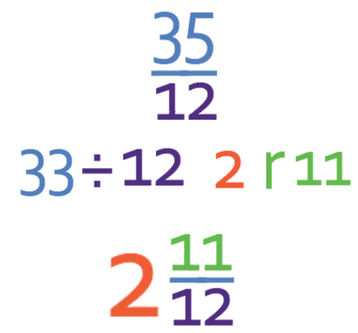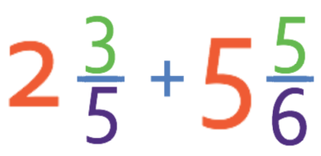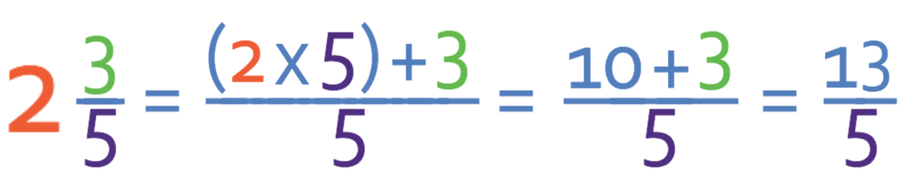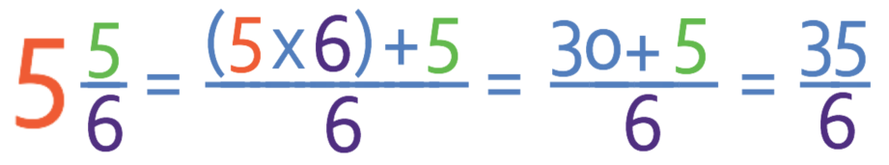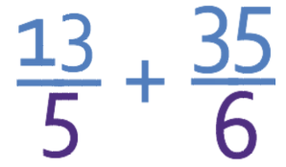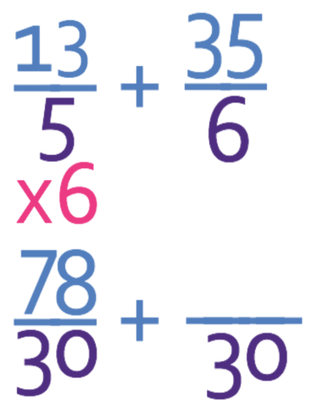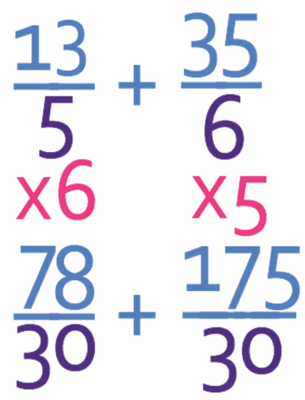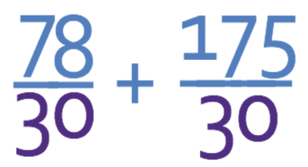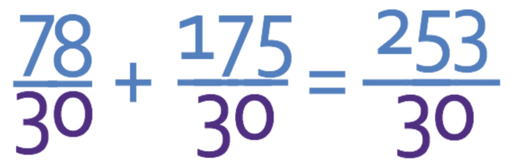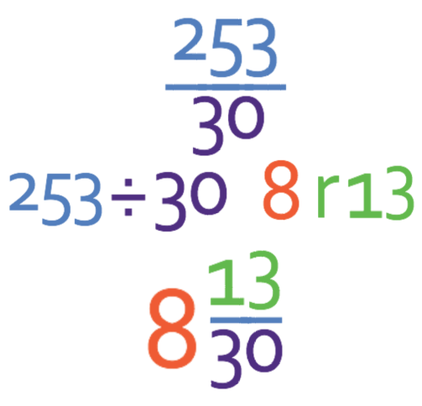1.3 I) Adding & Subtracting Mixed Numbers
Let’s have a few examples.
Complete the calculation below giving your answer as a mixed number in its simplest form.
The first step is to convert both of these mixed numbers into improper fractions. We do this by multiplying the wholes by the denominator of the fraction, and then we add the numerator of the fraction onto this number. The denominator of the fraction remains the same.
Let’s make the first fraction an improper fraction.
There are 4 wholes in this mixed number, so we multiply 4 by the denominator of the fraction (4), which gives us 16 (4 x 4). We then add 16 to the current numerator (3), which tells us that the new numerator is 19.
We now do the same with the second fraction.
There is 1 whole in the second fraction. To get the whole number into the fraction, we need to multiply the whole number (1) by the denominator of the fraction (6), which gives 6. We then need to add this number to the current numerator (5), which gives the new numerator as 11.
The calculation with both fractions as improper fraction is:
The denominators in the fractions above are not the same and this means that we are unable to subtract the fractions. Therefore, the next step in this question is to get the denominators the same. We do this by finding the lowest common multiple between 4 and 6, which is 12 (if you could not find the lowest common multiple between 4 and 6, you could cross multiply the fractions; multiply the numerator and the denominator of the first fraction by the denominator of the second fraction (6), and multiply the numerator and the denominator of the second fraction by the denominator of the first fraction (4). This will give the same answer but may take slightly longer as you will be dealing with higher numbers).
We are going to be creating equivalent fractions with the denominator of 12. Whenever we are creating equivalent fractions, we need to ensure that we multiply the numerator and the denominator by the same value.
Currently the denominator of the first fraction is 4 and we want it to be 12. Therefore, we will be multiplying the numerator and the denominator of the first fraction by 3. This means that the first fraction becomes 57/12.
We do the same for the second fraction. Currently, the second fraction has a denominator of 6 and we want this denominator to be 12. Therefore, we multiply the numerator and denominator by 2 (or double them). This means that the second fraction becomes 22/12.
As the denominators of the fraction are the same, we can carry out the calculation by taking the second numerator from the first numerator and keeping the denominator the same (the denominator stays as 12).
We now need to make sure that our fraction is in its simplest form and give it as a mixed number. It does not matter which one you do first.
I am going to make this fraction a mixed number first. A mixed number will have a number and a fraction. To obtain the number, we find out how many times the denominator fully goes into the numerator. The remainder then becomes the numerator for the fraction part of the mixed number.
Therefore, to obtain the whole number, I am looking to see how many times 12 fully go in 35, which is twice with a remainder of 11. Therefore, the mixed number is:
We now need to check if the fraction part of the mixed number can be simplified and we do this by dividing by any common factors between the numerator and the denominator. There are no common factors between 11 and 12, which means that our mixed number is in its simplest form. Therefore, the answer to this question is 2 11/12.
Complete the calculation below. Give you answer as a mixed number and in its simplest form.
The first part of the question is to make these two fractions improper fractions rather than mixed numbers. We get the whole number into the fraction by multiplying it by the denominator of the fraction that it is going in to. We then add this number to the original numerator to obtain the numerator for the improper fraction. The denominator of the fraction stays the same.
Therefore, for the first fraction, there are 2 whole numbers and the denominator is 5, which means that we will be multiplying 2 by 5 and this gives us 10. We then need to add the original numerator in the fraction part of the mixed number (3) to this number; the numerator for the improper fraction is 13 (10 + 3). The first fraction as an improper fraction is 13/5.
We do the same for the second fraction. We multiply 5 by 6, which gives us 30 and then we add the original numerator (5) to this value. The numerator for the new fraction is 35 (30 + 5). The second fraction as an improper fraction is 35/6.
The calculation with both of the fractions as improper fractions is:
In order to add (or subtract fractions), we need to have a common denominator. The common denominator is going to be the lowest number that both the current denominators (5 and 6) go into. The lowest number that both 5 and 6 go into is 30.
We now create equivalent fractions by multiplying the numerator and the denominator of the fractions by the same number. The denominator of the first fraction is 5 and in order for it to become 30, it needs to be multiplied by 6 and this means that we also need to multiply the numerator by 6. The first fraction becomes:
We now do the same for the second fraction. Currently the denominator of the second fraction is 6, which means that it needs to be multiplied by 5 for it to become 30. Therefore, we multiply the numerator by 5.
This gives us the calculation.
The denominators of the fraction above are the same and this means that we are able to add the numerators.
We now need to convert this fraction into a mixed number and simplify. It does not matter which one you do first, but I think that it is better to convert it into a mixed number and then simplify (if possible).
A mixed number has a number part and a fraction part. We obtain the number part of the mixed number by seeing how many times the denominator fully goes into the numerator (253 ÷ 30), which is 8. The numerator of the fraction part of the denominator is the remainder, which is 13. This means that the answer as a mixed number is:
We now need to check if the fraction part of the mixed fraction can be simplified and it cannot be simplified because there are no common factors between 13 and 30. Therefore, the final answer for this calculation is 8 13/30.