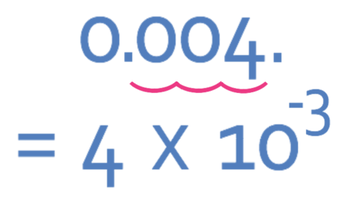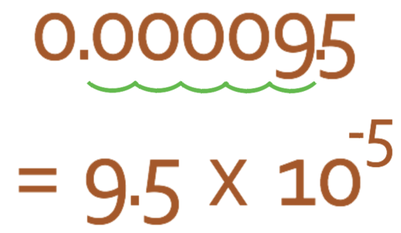1.7 B) Small Numbers
A number written in standard form will follow this form:
A in the form above is a number between 1 and 10 (1 ≤ A < 10). n is the power of 10.
When small numbers are written in standard form they have a negative value for n. For example, 4.5 x 10-2. A negative power can be written in the form as 1 divided by the positive power; 1/ 102. Here are the first 5 negative powers of 10.
100 = 1
10-1 = 1/101 = 1/10 = 0.1
10-2 = 1/102 = 1/100 = 0.01
10-3 = 1/103 = 1/1,000 = 0.001
10-4 = 1/104 = 1/10,000 = 0.0001
10-5 = 1/105 = 1/100,000 = 0.00001
Let’s now look at taking numbers out of standard form and putting numbers into standard form.
Taking Out of Standard Form
Example 1
Take what is written below out of standard form.
The best way to take a number out of standard form is to write out A. As n is negative for this number (n is -3), we add the 0’s in front of the number and this is because a negative value for n makes A smaller (when the value for n is positive, we write the number with many 0’s after the decimal place and this is because a positive value for n makes the number bigger).
The value for n is -3, which means that we are moving the decimal point 3 places towards the left.
Therefore, 7.6 x 10-3 written out of standard form is 0.0076.
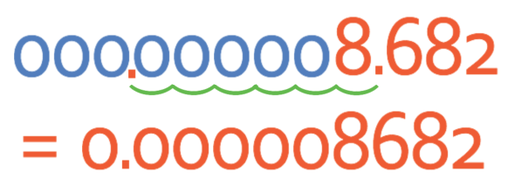
Example 2
Write the number below out of standard form.
As we have a negative value for n (n is -6), we will be adding the 0’s before the 8. As n is -6, this means that we are moving the decimal point 6 places to the left.
Therefore, the answer is 0.000008682.
Placing a Large Number into Standard Form
Example 3
Write the number below in standard form.
The first step is to choose our value of A, which needs to satisfy 1 ≤ A < 10. The value of A for 0.004 would be 4.
The next step is to see how many places we have to move the decimal point in order to give us 4.
From the diagram above, we can see that we move the decimal point 3 places to the right. Therefore, n is -3 (any movement of the decimal place to the right results in a negative n). So, 0.004 in standard form is 4 x 10-3.
Example 4
Write the number below in standard form.
Our value for A will be 9.5. We now need to find out how many places we moved the decimal point.
From the diagram above, we can see that we are moving the decimal point 5 places to the right, thus meaning that n is -5. Therefore, 0.000095 written in standard form is 9.5 x 10-5.
Final note
We are always able to check the answer that we have obtained. If we are placing a number into standard form, we can take our standard form answer out of standard form to see if we obtain the number that we started with. If we are taking something out of standard form, we can check that we have the correct answer by putting the number that we obtained back into standard form.
To save time, you may not want to fully take the number out/ back in to standard form, but it is definitely a good idea to check mentally.