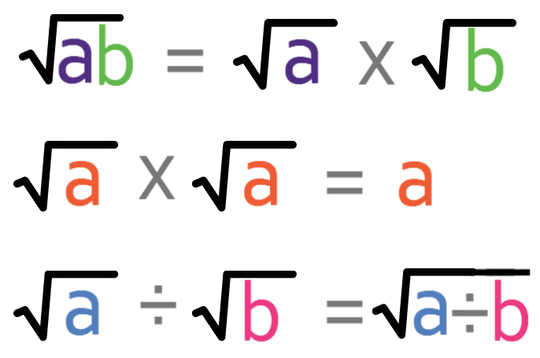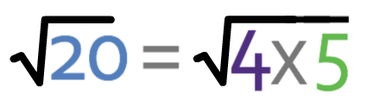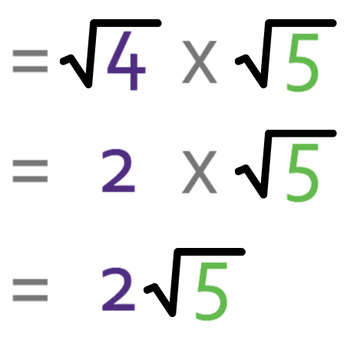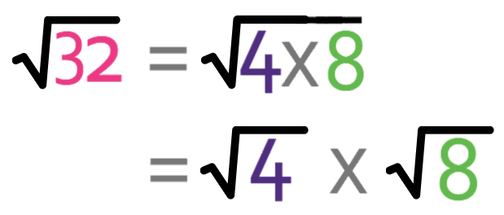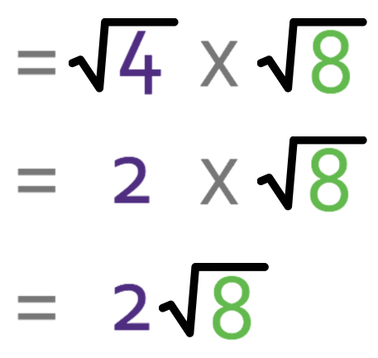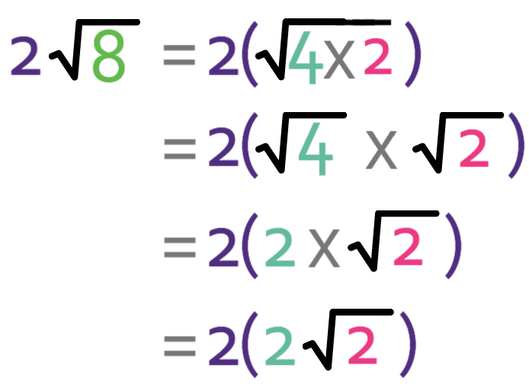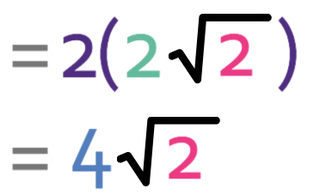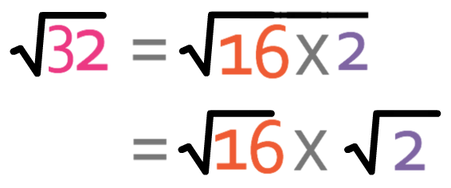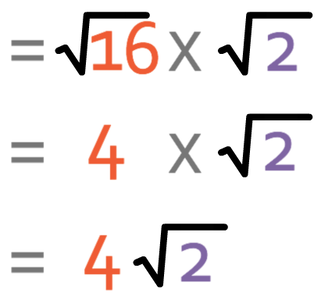Back to AQA Surds (H) Home
1.8 A) Introduction & Simplifying Surds
1.8 A) Introduction & Simplifying Surds
Surds are used to write irrational numbers, which are numbers that cannot be written as a fraction. Also, the number outside of the surd would not stop or recur. A surd includes any type of root, such as a square root or cube root. Usually you will only be dealing with square root surd.
Let’s have an example of a surd. An example is √2. If we want to write √2 in exact form it has to be written as √2. This is because it cannot be written as a fraction or as a decimal because it does not stop or recur.
Let’s have an example of a surd. An example is √2. If we want to write √2 in exact form it has to be written as √2. This is because it cannot be written as a fraction or as a decimal because it does not stop or recur.
The value of √2 is given above and the “…” at the end is to indicate the number would keep on going.
Surd Rules
There are a few different rules that we need to remember when we are looking at surds. These rules help us to simplify surds and we need to always make sure that we give our answers in their simplest form. Here are the 3 different rules:
There are a few different rules that we need to remember when we are looking at surds. These rules help us to simplify surds and we need to always make sure that we give our answers in their simplest form. Here are the 3 different rules:
We are going to be looking at the first rule in this section and the other two rules in the coming sections.
Example 1
Simplify:
Simplify:
We are able to use the first rule to help us simplify this surd. In order to simplify it, we are looking for factors of the number in the surd that are square numbers. We are then able to split the surd and take the square number out of the root. For the surd above, 4 is a square factor of 20 and this means that we can write our surd as:
The first rule then states that we are able to split the surd into two different surds that are multiplied by one another.
We know that √4 is 2 and this means that our surd becomes.
Whenever you have your final answer, it is a good idea to check that the number left in the surd does not have any more square factors in it. There are no square factors in 5, which means that 2√5 is our simplified surd.
Example 2
Simplify:
Simplify:
To simplify the surd above, we need to find factors of 32 that are square numbers. We will then be able to take the square factors out of the square root, thus simplifying the surd. The simplifying of surd is similar to the simplifying of fractions in the sense that we do not have to get to the final answer straight away; instead we can simplify bit by bit. This means that we do not need to find the highest square factor that goes into 32. Instead, we are able to find smaller factors and then check if there are any more square factors in the answer that we obtain.
For example, 4 is a factor of 32. This means that we are able to write √32 as:
For example, 4 is a factor of 32. This means that we are able to write √32 as:
We know that √4 is 2, so our surd becomes:
We now need to check whether the number that is in our surd has anymore square factors that go into it. The number in the surd is 8 and 4 is a factor of 8.
We now need to multiply what is inside the bracket by 2. The best way to multiply brackets that contain surds is to imagine that the surd is an unknown. For example, it would be very easy to expand the bracket 2(2x) because we would just multiply the numbers, which would mean that we would have 4x. This is exactly the same with a surd; we multiply the two numbers (the 2 on the outside of the bracket and the 2 that is next to the surd), which tells us that we have 4 lots of the surd. Therefore, the simplified surd is 4√2.
Alternatively, you might have seen that the highest square factor in 32 is 16. Therefore, our surd can be written as:
We know that √16 is 4, so our surd becomes:
This gives the same answer as before.
It is much easier to simplify surds by looking for the highest square number that goes into the number inside the surd. This is because you get to the answer quicker and there is fewer calculations, which means there is less chance of making an error.
It is much easier to simplify surds by looking for the highest square number that goes into the number inside the surd. This is because you get to the answer quicker and there is fewer calculations, which means there is less chance of making an error.
Example 3
Simplify:
Simplify:
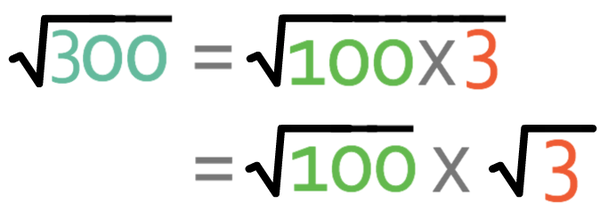
I am going to simplify this surd by looking for the highest square factor that goes into the 300. The highest square factor is 100, which means that the surd becomes:
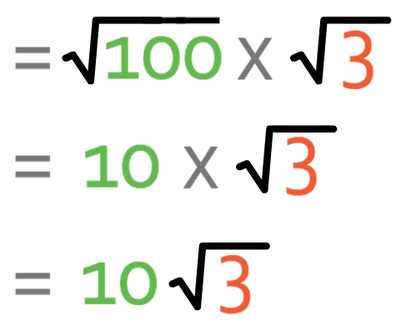
√100 is 10, which means that our surd becomes:
Therefore, the simplified surd is 10√3.
If you were unable to find the highest square factor, you could have found any square factor, simplified and then check your surd for anymore square factors. 25 is a square factor of 300.
If you were unable to find the highest square factor, you could have found any square factor, simplified and then check your surd for anymore square factors. 25 is a square factor of 300.
√(25 x 12)
√25 x √12
5 x √12
5√12
√25 x √12
5 x √12
5√12
We now need to check to see if there are any more square factors in the number in the surd. 4 is a factor of 12 and 4 is also a square number, which means that we can simplify our surd further.
5[√(4 x3)]
5[√4 x √3]
5[2 x √3]
5[2√3]
5[√4 x √3]
5[2 x √3]
5[2√3]
We now need to multiply out the bracket, which we do by multiplying the numbers that are not in the surd; we multiply the 5 and the 2. This means that the simplified surd is 10√3 and this is exactly the same as we found earlier.
5(2√3)
10√3
10√3