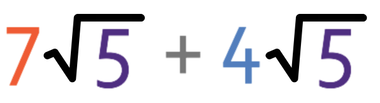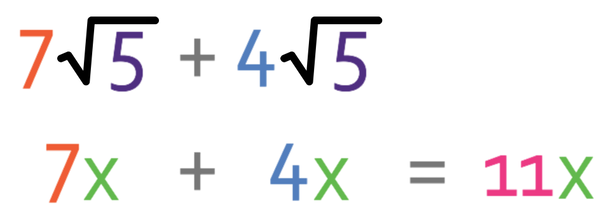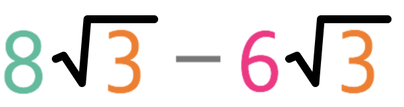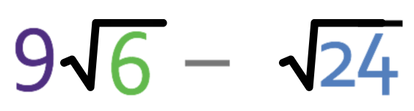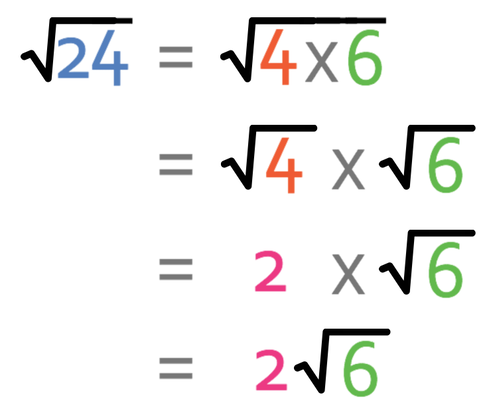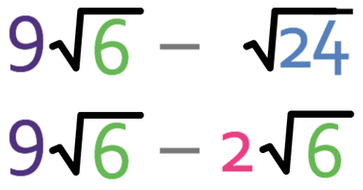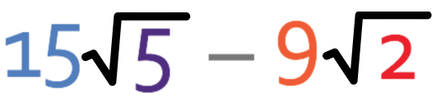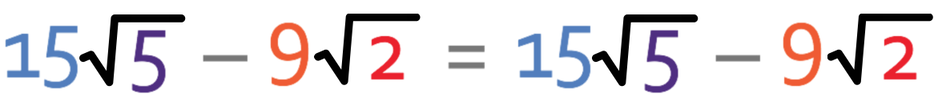Back to AQA Surds (H) Home
1.8 E) Adding & Subtracting Surds
1.8 E) Adding & Subtracting Surds
We are able to add and subtract surds if the numbers inside the surds are the same. If the numbers inside the surds are not the same, we may be able to simplify the surds so that they are the same.
The best way to add or subtract surds that have the same numbers inside the surds is to think of the surds as an unknown and to just add or subtract the numbers that are on the outside of the surd.
The best way to add or subtract surds that have the same numbers inside the surds is to think of the surds as an unknown and to just add or subtract the numbers that are on the outside of the surd.
Example 1
Complete the calculation below.
Complete the calculation below.
The numbers inside both of the surds are the same; they are both 5. Let’s let √5 equal x, which means that we can replace all of the √5’s in the calculation with x’s. The calculation becomes:
This gives us 11x. We can now replace the x with √5, which means that the answer is 11√5.
Example 2
Complete the calculation below.
Complete the calculation below.
The numbers inside the surds are the same (both are 3), which means that we can take the numbers on the outside of the surds; we will be taking 6 away from 8. This means that the answer is 2√3.
Example 3
Complete the calculation below.
Complete the calculation below.
The numbers inside the surds are not the same. It may be the case that one (or both) of the surds may be able to be simplified so that the numbers inside the surds become the same. When the numbers inside the surds are the same, we then add or subtract as usual.
We simplify surds by looking for square factors for the numbers inside of the surds. The first surd cannot be simplified because there are no square factors in 6. The second surd can be simplified because 4 is a square number and it is a factor of 24. This means that we can simplify the second surd.
We simplify surds by looking for square factors for the numbers inside of the surds. The first surd cannot be simplified because there are no square factors in 6. The second surd can be simplified because 4 is a square number and it is a factor of 24. This means that we can simplify the second surd.
We can replace √24 with 2√6.
We are now able to complete the calculation because both of the numbers inside the two surds are 6.
The answer to the question is 7√6 and it is in its simplest form.
Example 4
Complete the calculation below.
Complete the calculation below.
The numbers inside the surds are not the same. We need to check if we can simplify any of the surds to make them the same. However, we cannot simplify either of the surds because there are no square factors in 5 and 2. This means that the answer to this question is the question; the answer is 15√5 – 9√2. Type this calculation into the calculator and it will give you 15√5 – 9√2.
If you type this question into a calculator, the calculator will give you the answer 15√5 – 9√2.
This is question is a bit of a trick question because the answer is the question. You probably won’t get a question like this in the exam, but I wanted to illustrate the point that you can only add or subtract surds when the numbers inside the surds are the same.
This is question is a bit of a trick question because the answer is the question. You probably won’t get a question like this in the exam, but I wanted to illustrate the point that you can only add or subtract surds when the numbers inside the surds are the same.