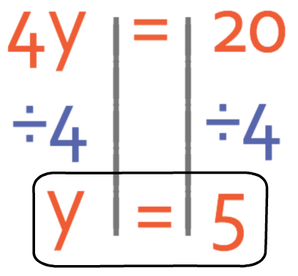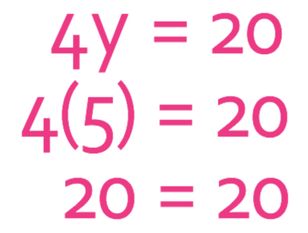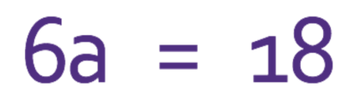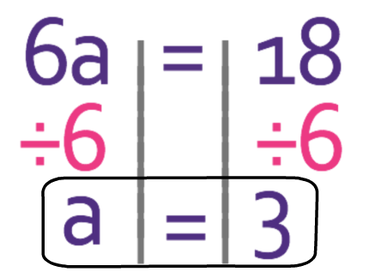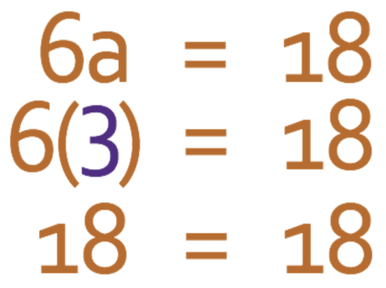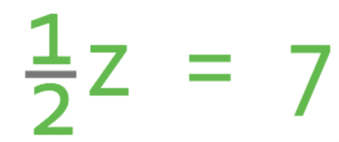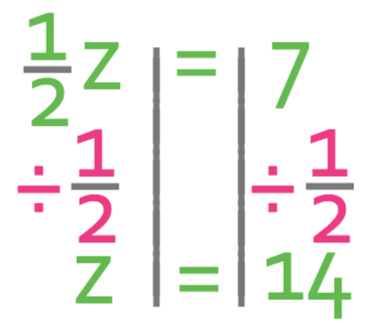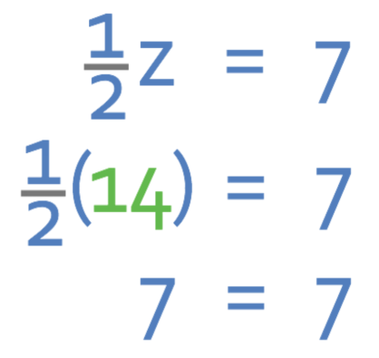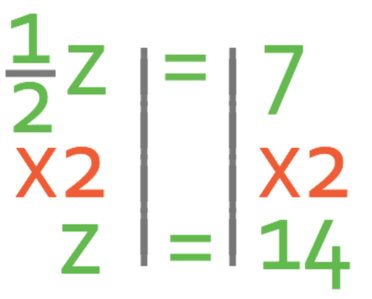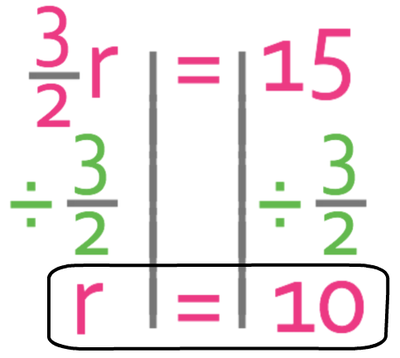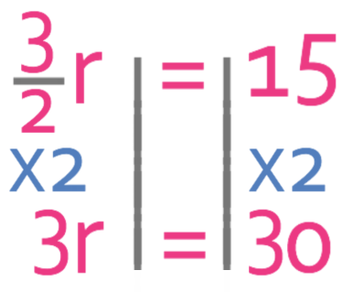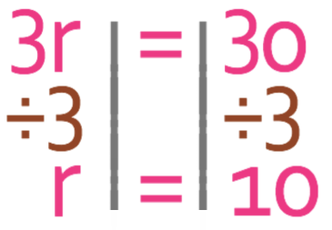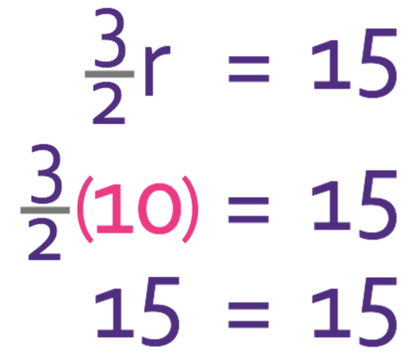Back to AQA Linear Equations (H) Home
2.2 B) Linear Equations: Multiples of Unknowns
2.2 B) Linear Equations: Multiples of Unknowns
When we have an equation where a multiple of unknowns is equal to a number, we find the value of the unknown that we are looking for by dividing by the number of unknowns that we have (which is the coefficient for the unknowns).
When we are using this strategy, we need to make sure that we have all of the unknowns on one side of the equation and all of the numbers on the other side of the equation. All the examples that we look at in this section will be like this, but in the next section, we will need to modify the equation so that this is the case.
When we are using this strategy, we need to make sure that we have all of the unknowns on one side of the equation and all of the numbers on the other side of the equation. All the examples that we look at in this section will be like this, but in the next section, we will need to modify the equation so that this is the case.
Example 1
Solve the equation below.
Solve the equation below.
The left side of the equation tells us that 4 lots of the unknown y is equal to 20. However, we do not want to know what 4y is; instead we want to know what y is. Therefore, we divide both sides of the equation by 4.
Therefore, y is 5. Like before, we can check that our answer is correct by subbing y as 5 back into the equation.
This equation holds, which means that the value that we found for y is correct; y is 5.
Example 2
Find the value of a.
Find the value of a.
The left side of the equation tells us that 6 lot of a is 18. We want to find the value of a and not 6a. Therefore, we divide both sides of the equation by 6.
Therefore, a is equal to 3. We can check that a is 3 by subbing a as 3 into the original equation. The working is shown below.
This equation works, which means that a is 3.
Example 3
Find the value for z in the equation below.
Find the value for z in the equation below.
There are two different method that we can use to find the value of an unknown when the unknown has a fraction as its coefficient.
Method 1
Let’s use the first method; dividing both sides by the coefficient of the unknown. The coefficient of z is ½, thus meaning that we divide both sides of the equation by ½.
- One method is to divide both sides of the equation by the coefficient of the unknown.
- The other method is to multiply both sides of the equation by the denominator of the coefficient of the unknown. The whole point of doing this is to get rid of the fraction for the unknown. We then divide both sides of the equation by what was the numerator of the coefficient of the unknown if the numerator of the coefficient is not 1. This method is easier to use when we are unable to use a calculator.
Method 1
Let’s use the first method; dividing both sides by the coefficient of the unknown. The coefficient of z is ½, thus meaning that we divide both sides of the equation by ½.
This tells us that z is 14. We can check that this is correct by subbing in z as 14 into the equation.
The above equation holds, which means that we have found the correct value for z.
Method 2
The other method is to multiply both sides by the denominator of the coefficient of the unknown, and then divide both sides by what was the numerator of the coefficient of the unknown (if the numerator is not 1). The coefficient of the unknown is ½. The denominator of the coefficient is 2. Therefore, we multiply both sides of the equation by 2.
Method 2
The other method is to multiply both sides by the denominator of the coefficient of the unknown, and then divide both sides by what was the numerator of the coefficient of the unknown (if the numerator is not 1). The coefficient of the unknown is ½. The denominator of the coefficient is 2. Therefore, we multiply both sides of the equation by 2.
The numerator of the coefficient was 1. Therefore, we do not need to divide by the numerator because dividing anything by 1 is the same; 14 divided by 1 is 14.
This means that z is 14, which is exactly the same answer that we found using the other method.
This means that z is 14, which is exactly the same answer that we found using the other method.
Example 4
Find the value of r.
Find the value of r.
Like the question before, there are two methods to obtain the value of r.
Method 1
The first method is to divide both sides by the coefficient of the unknown, which means that we are dividing by 3/2 (1.5).
For the above question, it was not too hard dividing by 3/2, but you may sometimes be given a fraction that is much harder, which means that you may find the next method easier.
Method 2
In the next method, we multiply both sides of the equation by the denominator of the coefficient of the unknowns. We then divide both sides by what was the numerator of the coefficient of the unknowns providing that the numerator is not 1. The coefficient of the unknowns is 3/2 and the denominator is 2. Therefore, we multiply both sides by 2.
The next step is to divide by what was the numerator of the coefficient of the unknowns, which is 3. You can also see that we need to divide by 3 because we want to know what r is and not what 3r is.
Like before, we can check the value of r by subbing it into the initial equation.
This equation works, which means that we have the correct value for r.