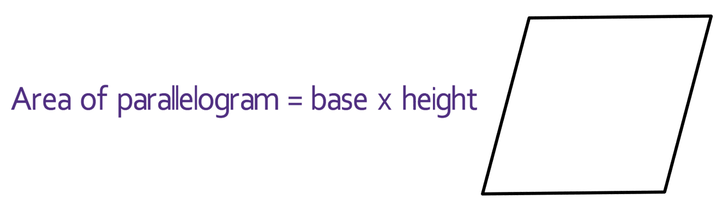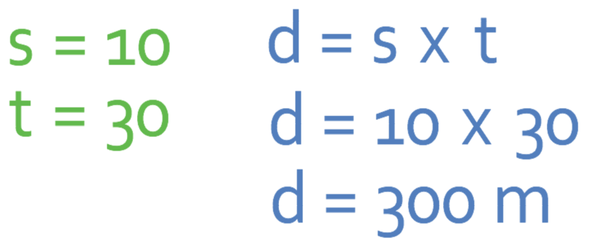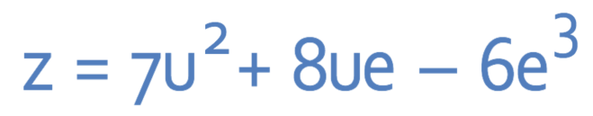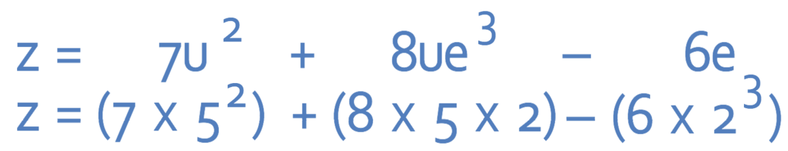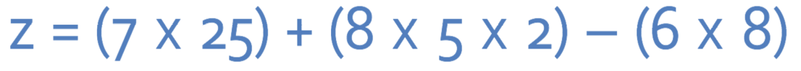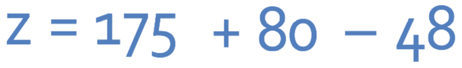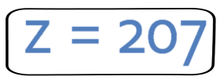Back to AQA Algebraic Formulae (H) Home
2.3 A) Formulas Introduction
2.3 A) Formulas Introduction
A formula shows the relationship between different variables. There are many formulas that we use when we are working out areas of shapes.
For example, the formula that we use to work out the area of a triangle is:
For example, the formula that we use to work out the area of a triangle is:
Another example of a formula for a shape is the formula that is used to work out the area of a parallelogram, which is given below:
There are many more formulas that you will come across when you are working out the volume, area or perimeter of shapes.
It is not just shapes that have formulas. We also have formulas for a variety of other variables. For example, the formula below is the formula for working out the distance travelled.
It is not just shapes that have formulas. We also have formulas for a variety of other variables. For example, the formula below is the formula for working out the distance travelled.
Where:
The whole point of having a formula is so that we are able to find the value of an unknown variable providing that we are given the values of all other variables except the variable that we are asked to find (we are only able to find an unknown when there is only one unknown in the question). We find this unknown variable by subbing in the values of all of the other variables that we are given.
- d is the distance travelled in metres
- s is the speed in metres per second
- t is the time in seconds
The whole point of having a formula is so that we are able to find the value of an unknown variable providing that we are given the values of all other variables except the variable that we are asked to find (we are only able to find an unknown when there is only one unknown in the question). We find this unknown variable by subbing in the values of all of the other variables that we are given.
Example 1
For example, an object is moving at a speed of 10 m/s for 30 seconds. What is the distance travelled by the object?
The question is asking us to find the value of d. The question has given us the value of s, which is 10 m/s, and the value of t, which is 30 seconds. We are able to obtain the distance travelled by subbing in s as 10 and t as 30 into the formula.
For example, an object is moving at a speed of 10 m/s for 30 seconds. What is the distance travelled by the object?
The question is asking us to find the value of d. The question has given us the value of s, which is 10 m/s, and the value of t, which is 30 seconds. We are able to obtain the distance travelled by subbing in s as 10 and t as 30 into the formula.
The object has travelled 300 m during the 30 seconds.
Example 2
Let’s have another example of a formula. The formula that we are going to use is given below.
Let’s have another example of a formula. The formula that we are going to use is given below.
Find the value of z when u is 5 and e is 2.
We obtain the value of z by subbing in of u as 5 and e as 2. Whenever we are working with formulas, we need to be very careful to follow the rules of BODMAS/ BIDMAS (Brackets, Other (or indices) Division, Multiplication, Addition and Subtraction). BODMAS means that we need to deal with all of the different operations in order. Let’s sub the values for u and e into the equation to find the value of z; we sub in u as 5 and e as 2.
We obtain the value of z by subbing in of u as 5 and e as 2. Whenever we are working with formulas, we need to be very careful to follow the rules of BODMAS/ BIDMAS (Brackets, Other (or indices) Division, Multiplication, Addition and Subtraction). BODMAS means that we need to deal with all of the different operations in order. Let’s sub the values for u and e into the equation to find the value of z; we sub in u as 5 and e as 2.
I have added brackets into the formula to make it easier for us to see what is happening. We need to work out each bracket seperately following the rules of BODMAS in each of the 3 brackets. The first step is to work out the indices; we work with the 52 and the 23.
We can now multiply out each of the three different brackets.
We are now able to add the 175 and 80 together.
Finally, we take the 48 from 255.
Therefore, the value of z is 207 when u is 5 and e is 2.