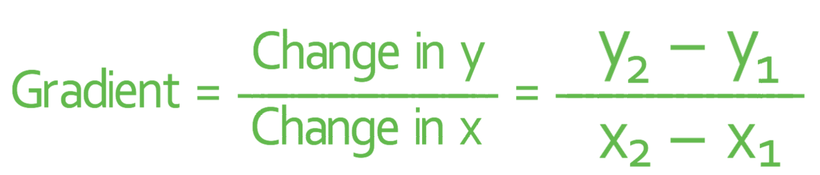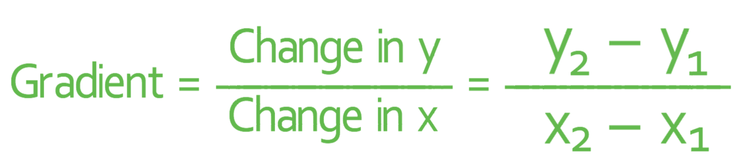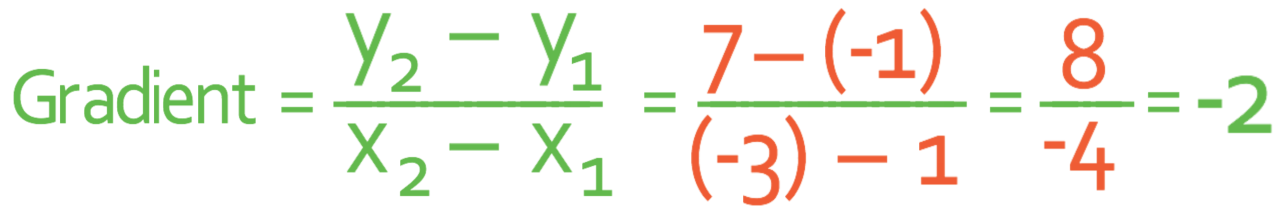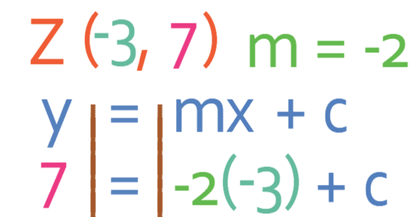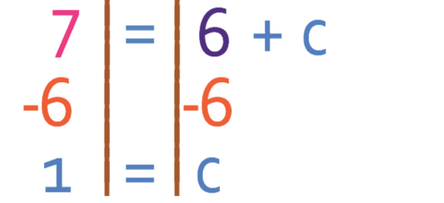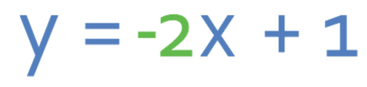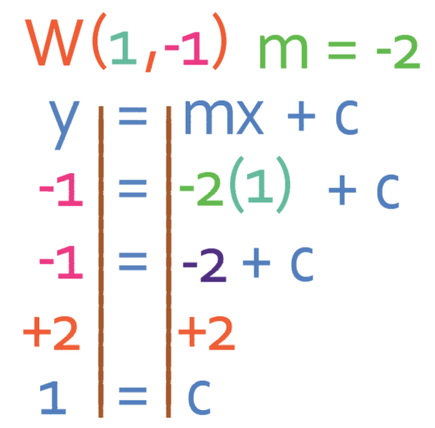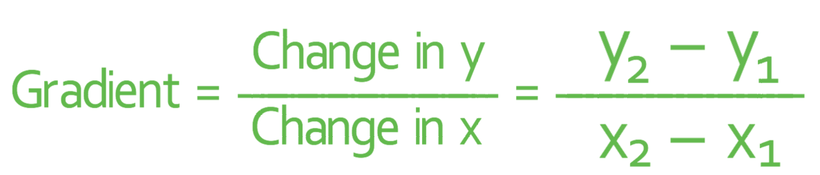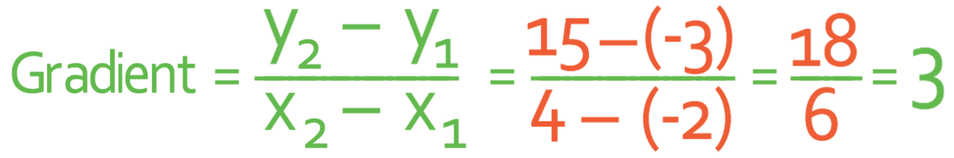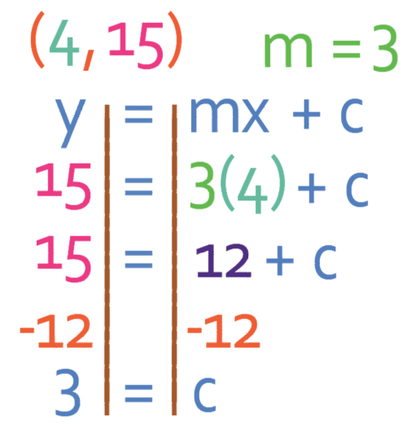Back to AQA Linear Graphs (H) Home
2.5 K) Finding the Equation of a Line – 2 Points
2.5 K) Finding the Equation of a Line – 2 Points
In section before this, we looked at questions where we were asked to find the equation of a line when we are given the gradient of the line and a point that lies on the line. In this section, we are going to be finding the equation of lines when we are given two points that lie on the line.
We answer questions like this by finding the gradient of the line first. We are able to find the gradient of the line because we are given two points that lie on the line. In order to find the gradient from two points, we will be using the following formula:
We answer questions like this by finding the gradient of the line first. We are able to find the gradient of the line because we are given two points that lie on the line. In order to find the gradient from two points, we will be using the following formula:
After we have found the gradient of the line, we find the value of c by subbing the x and y values from one of the coordinates into y = mx + c (with m being the value for the gradient that we have just found). It does not matter which coordinate we sub into the equation because both of them will give the same value for c. The final step is to write the equation with both the value of m and c subbed in.
Let’s have some examples.
Let’s have some examples.
Example 1
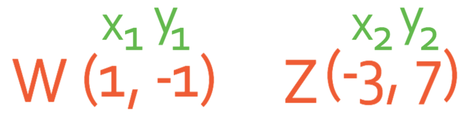
The points W and Z lie on a line, what is the equation of the line? The coordinates for W are (1, -1) and the coordinates for Z are (-3, 7).
The first step to answering this question is to find the gradient of the line. We do this by using the following formula.
The points W and Z lie on a line, what is the equation of the line? The coordinates for W are (1, -1) and the coordinates for Z are (-3, 7).
The first step to answering this question is to find the gradient of the line. We do this by using the following formula.
We now need to label the coordinates as 1 and 2; I am going to make Z point 1 and W point 2.
The next step is to sub the values into their appropriate place in the gradient formula and find the gradient. If we have any negative values/coordinates, it is best to place them inside brackets. This is so that we do not make any mistakes with the signs.
The gradient of the line is -2. We now know that the equation of the line will take the form y = -2x + c. We find the value of c by subbing in the x and y values for one of the coordinates that lies on the line; it does not matter which of the two coordinates that I sub in. Let’s use the coordinates at point Z. Point Z has the coordinates (-3, 7), which means that we are subbing in x as -3 and y as 7.
Note: the multiplication of two negative numbers makes a positive; -2(-3) is positive 6. We therefore get:
Therefore, the equation of the line is:
To prove that it does not matter which coordinates we use to find the value of c, I am now going to find the value of c by using point W. Prior to knowing what c is, we knew that the equation of the line was y = -2x + c. Point W has the coordinates (1, -1), so we sub in x as 1 and y as -1 into y = -2x + c. We then solve to find the value of c.
This gives us a value of c as 1, thus meaning that the line has the equation y = -2x + 1. This is exactly the same equation as we found when using point Z.
When are choosing the point to sub into the equation to find the value of c, choose the point that looks nicer with respect to the size of the numbers (go for smaller ones rather than larger ones) and with respect to the signs (it is easier to work with positive coordinates rather than negative coordinates).
When are choosing the point to sub into the equation to find the value of c, choose the point that looks nicer with respect to the size of the numbers (go for smaller ones rather than larger ones) and with respect to the signs (it is easier to work with positive coordinates rather than negative coordinates).
Example 2
A line passes through the points (-2, -3) and (4, 15). What is the equation for the line?
Like the example before, the first step is to find the gradient of the line, which we do by using the formula below.
A line passes through the points (-2, -3) and (4, 15). What is the equation for the line?
Like the example before, the first step is to find the gradient of the line, which we do by using the formula below.
We are going to be using the two points given in the question. I am going to have point 1 as (-2, -3) and point 2 as (4, 15).
We now sub the values into their appropriate places into the gradient formula.
The gradient of the line is 3. We now know that the equation of the line will be y = 3x + c and we need to find the value of c. We find the value of c by subbing one of the coordinates in. It does not matter which coordinate we sub in because we will get the same value for c from both. I am going to sub in (4, 15) because both of the coordinates are positive, which means that they will be slightly easier to deal with. So, I will sub in x in as 4 and y in as 15.
c is equal to 3. This means that the line has the equation: