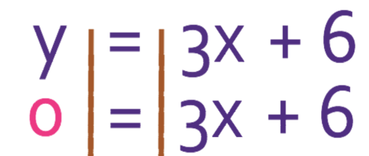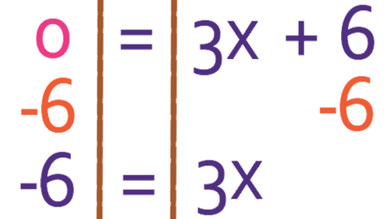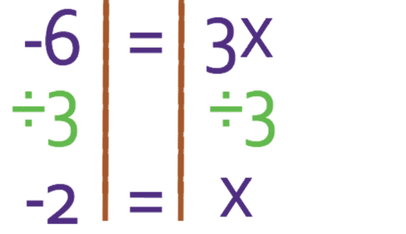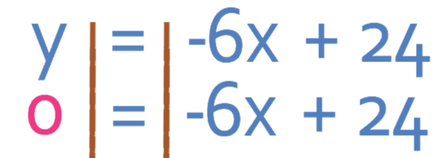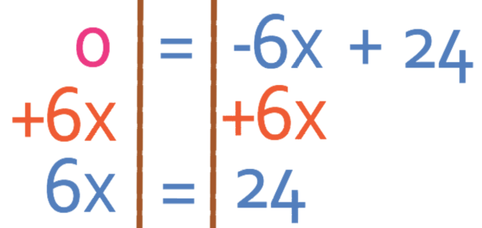Back to AQA Linear Graphs (H) Home
2.5 M) Finding the Root of a Linear Line
2.5 M) Finding the Root of a Linear Line
A root is where a line (or a curve) crosses the x axis. Linear lines only have one root (other equations such as quadratic and cubic functions can have more than one root).
We can find a root in two ways; one method is to find the root algebraically and the other method is to find a root graphically.
We can find a root in two ways; one method is to find the root algebraically and the other method is to find a root graphically.
Finding the Root Algebraically
A root is where the line intercepts the x-axis. The y coordinate for any point on the x-axis is zero. Therefore, we can find the root of an equation algebraically by subbing in y as zero into the equation.
Example 1
What is the root for the equation y = 3x + 6.
We find the root for this equation by subbing in y as 0. This gives us the equation:
A root is where the line intercepts the x-axis. The y coordinate for any point on the x-axis is zero. Therefore, we can find the root of an equation algebraically by subbing in y as zero into the equation.
Example 1
What is the root for the equation y = 3x + 6.
We find the root for this equation by subbing in y as 0. This gives us the equation:
We then find the value of x by solving the equation. We do this by isolating all of the x’s; we get all of the x’s to one side of the equation and all of the numbers to the other side. There are more x’s on the right, so it makes sense to have x’s on the right and numbers on the left. Therefore, we move the 6 from the right side of the equation to the left, which we can do by taking 6 from both sides of the equation.
We now have all of the x’s on one side and all of the numbers on the other side. The next step is to divide both sides by the coefficient of x, which is 3 (we divide by 3 because we want to find the value of x and not 3x).
Therefore, the root of the equation has an x coordinate of -2. The y coordinate for the root was 0, so this means that the root has the coordinates (-2, 0).
Finding the Root Graphically
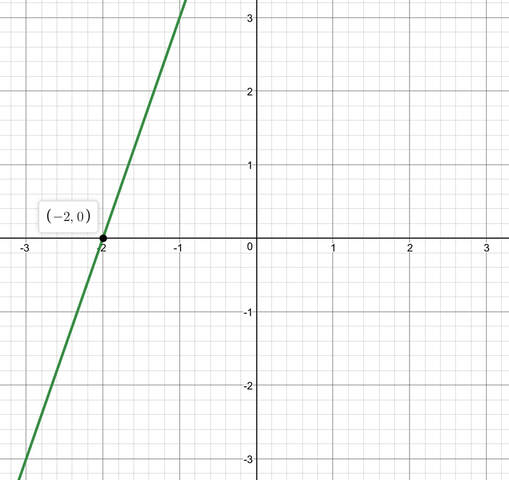
The second method is to find the root graphically, which is where we plot the line and find the x coordinate for where the line crosses the x axis. The graph from example 1 is plotted below.
Finding the Root Graphically
The second method is to find the root graphically, which is where we plot the line and find the x coordinate for where the line crosses the x axis. The graph from example 1 is plotted below.
From the above graph, we can see that the line crosses the x-axis at (-2, 0). Therefore, the root of the equation is where x is -2.
Example 2
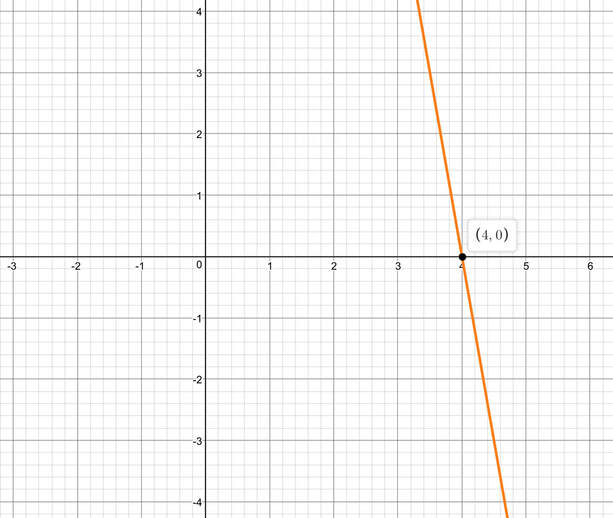
The line that is plotted on the graph below has the equation y = -6x + 24. What is the root of the line below?
The line that is plotted on the graph below has the equation y = -6x + 24. What is the root of the line below?
The line intersects the x axis at (4,0). Therefore, the root of this equation is 4.
Let’s now find the root algebraically. We solve it algebraically by subbing in y as 0 into the equation of the line.
Let’s now find the root algebraically. We solve it algebraically by subbing in y as 0 into the equation of the line.
The easiest way to find the value of x is to get all of the x’s to the side of the equation that currently has more x’s. Currently, there are more x’s on the left side of the equation than the right; 0x is more x’s than -6x. Therefore, we are going to get all of the x terms to the left and all of the numbers to the right. We need to move the -6x from the right side of the equation to the left and we do this by doing the opposite; we add 6x to both sides.
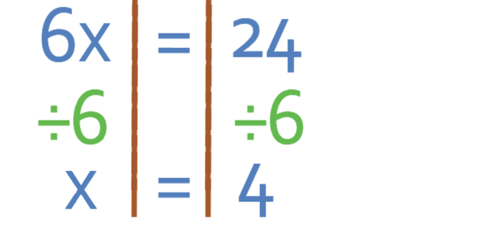
We then divide both sides by 6 (the coefficient of x) because we want to find the value of x and not 6x.
Therefore, the root for the equation is 4, which is the same answer as the graphical method.
Final Note
Usually, you will not be given a diagram of the line on a graph, which means that you will be unable to spot the root straight away. When this is the case, it is best to find the root by subbing in y as 0 and solving to find the value of x. This is because the graphical method of plotting the line and finding where the line passes through the x axis will take considerably longer to find the root of the equation compared with finding the root algebraically.
Usually, you will not be given a diagram of the line on a graph, which means that you will be unable to spot the root straight away. When this is the case, it is best to find the root by subbing in y as 0 and solving to find the value of x. This is because the graphical method of plotting the line and finding where the line passes through the x axis will take considerably longer to find the root of the equation compared with finding the root algebraically.