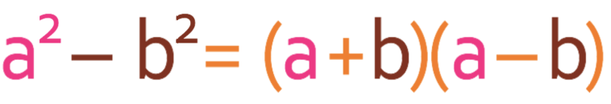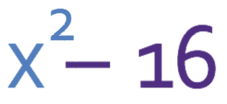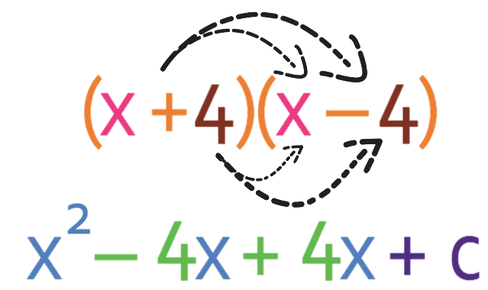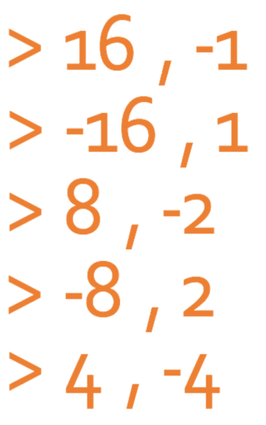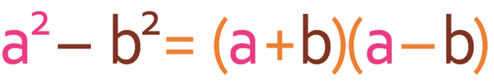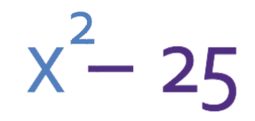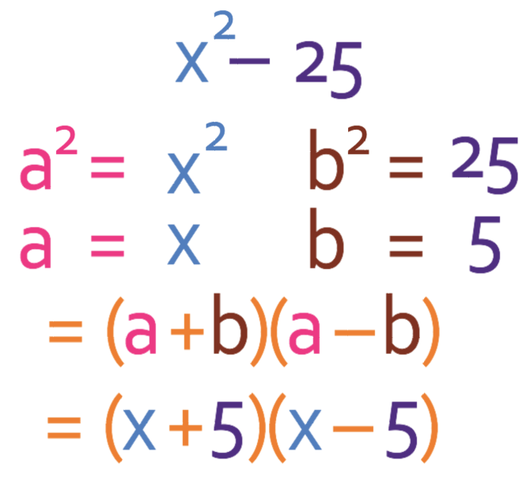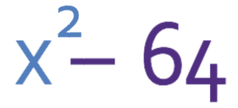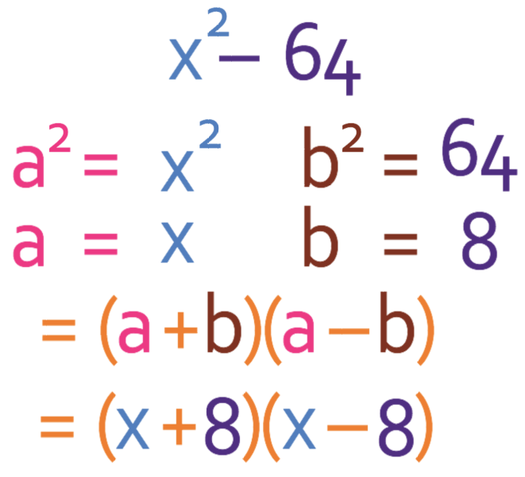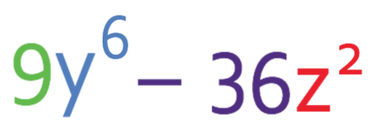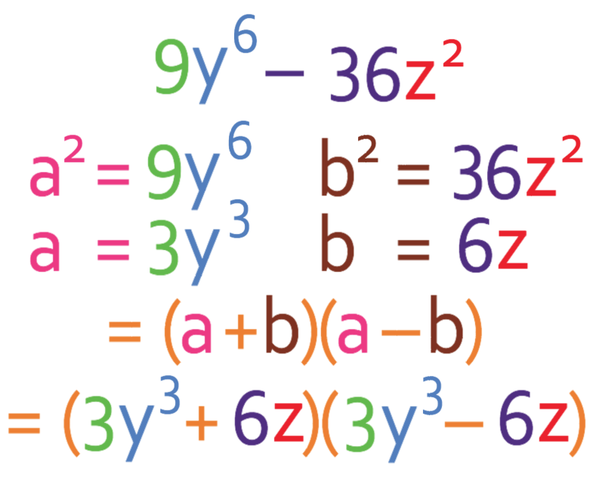2.6 C) The Difference of Two Squares
Whenever we have an expression that has a “square term” minus another “square term”, we are able to factorise the expression by using the following rule.
Factorise the expression:
These two terms are both square terms; x2 is the square of x and 16 is the square of 4. We can factorise this expression into two brackets. The first term in each of the brackets will be the square root of the positive term. We then add the square root of the term that we are taking in the first bracket and take this square root in the second bracket. The factorised expression is:
The order of the brackets does not matter; we could have written the factorised expression as (x – 4)(x + 4). It is probably best to always add in the first bracket and take in the second bracket; this is so that it is easier to remember the difference of two squares rule when you do the same every time.
To check that we have factorised correctly, we can multiply out the brackets above. I will do this by using FOIL (First, Outer, Inner, Last).
We could have factorised this expression by using the method that was discussed in the previous section; if a is 1, we are looking for two numbers that multiply together to give c and add together to give b. For the expression x2 – 16, a is 1, b is 0 and c is -16. Therefore, we are looking for two numbers that multiply together to give -16 and add together to give 0.
Here are the pairs of number that multiply together to give -16:
Of these pairs, the only pair that adds together to give 0 is 4 and -4. Therefore, the factorised expression is:
This is the same brackets as we found earlier. It is so much quicker to factorise the difference of two square expressions by using the general form rather than factorising by looking for two numbers that multiply to give c and add to give b.
The general rule for the difference of two squares is given below.
Factorise:
a2 in this expression is x2, which means that a is x. b2 is 25, which means that b is 5.
Therefore, the factorised expression is:
Factorise:
a2 in the above expression is x2, which means that a is x. b2 in the above expression is 64, which means that b is 8.
Therefore, the factorised expression is:
Factorise:
This is a slightly more complex expression to factorise, but the process of factorising is exactly the same as earlier. In this expression a2 is 9y6. In order to find a, we square root a2; we square root 9y6. The easiest way to square root 9y6 is to square root the number and then square root the unknown. The number is 9 and the square root of 9 is 3. To square root an unknown that is to the power of something, we multiply the power by ½. Therefore, the square root of y6 is y3 (y ½ x 6 = y3). We now combine these two square roots, which tells us that a is 3y3. We can check that we have square rooted correctly by squaring the square root; 3y3 x 3y3 = 9y3+3 = 9y6).
b2 in the expression is 36z2. We find out what b is by squaring rooting 36z2. The easiest way to do this is to square root the number and then the unknown. The square root of 36 is 6, and the square root of z2 is z. Therefore, b is 6z.
We can now sub the values for a and b into the generic formula for the difference of two squares; we sub a in as 3y3 and b as 6z.