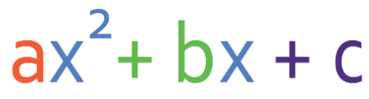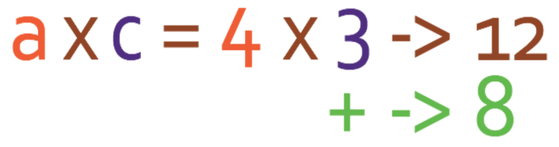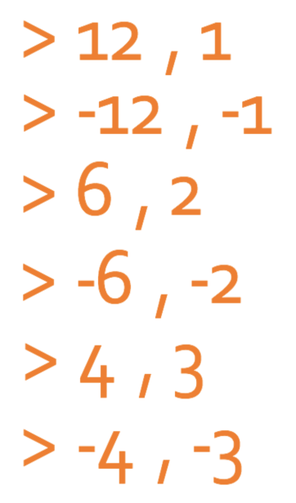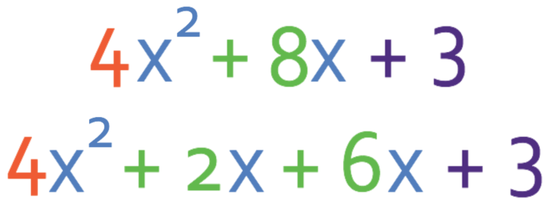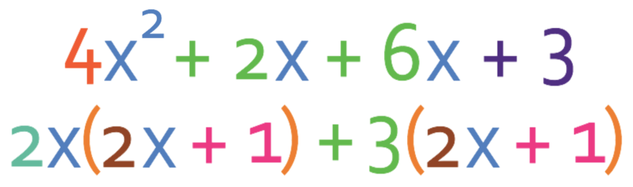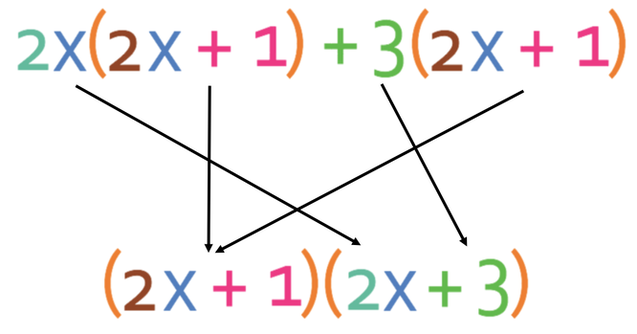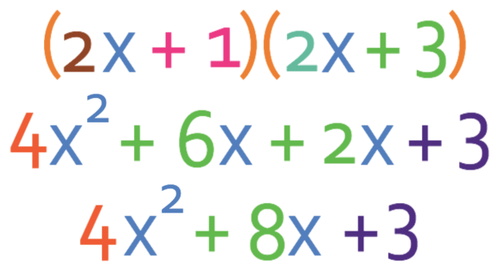Back to AQA Quadratic Equations: Factorising (H) Home
2.6 D) Factorising Quadratics (A ≠ 1) – Part 1
2.6 D) Factorising Quadratics (A ≠ 1) – Part 1
Quadratic equations are generally written in the form:
The sections before this looked at factorising quadratic equations where a was 1. When the value of a is 1, each of the brackets will have an x in them and the numbers in each of the brackets are found by finding two numbers that multiply together to give the value of c and add together to give the value of b.
However, when the value for a is not 1, we need to use a different technique to factorise the expression. This technique is best explained through an example.
However, when the value for a is not 1, we need to use a different technique to factorise the expression. This technique is best explained through an example.
Example 1
Factorise the quadratic expression below.
Factorise the quadratic expression below.
The first step to factorise the quadratic expression is to multiply a (the coefficient of x2) by c (the constant term; the number at the end). a in the expression is 4 and c is 3. When we multiply these two together we get 12.
We are now looking for two numbers that add together to give the value of b, which is 8 and multiply together to give 12 (a x c).
Here are the pairs of numbers that multiply to give 12:
The only pair that adds to give 8 is 6 and 2. The whole point of finding this pair of numbers is so that we can replace 8x in the expression with 6x + 2x (which still gives 8x). It does not matter which way we sub 6x + 2x into the expression; we could have subbed it in as 2x + 6x. The expression becomes:
The next step is to factorise the first two terms and the last two terms separately. When we are factorising the first two terms and the last two terms, we should get the same factors inside the bracket.
We can see from the above expression that both of the brackets are (2x + 1).
The first bracket in the final factorise expression will be the common factor of (2x + 1). The second bracket is the terms that are outside each of the brackets.
The first bracket in the final factorise expression will be the common factor of (2x + 1). The second bracket is the terms that are outside each of the brackets.
We are able to check whether we have factorised correctly by expanding the brackets. The working for the expanded brackets is shown below.
The expanded brackets gives the same expression that we were factorising. This means that we have factorised correctly.