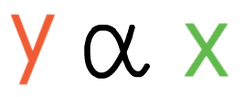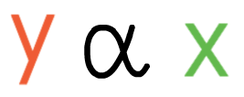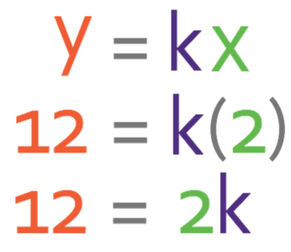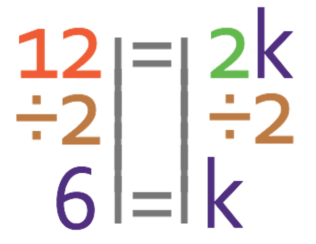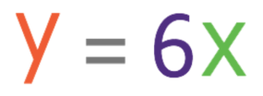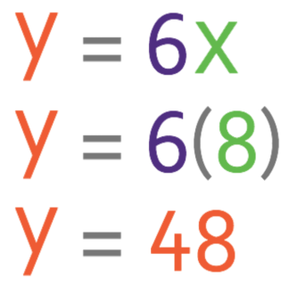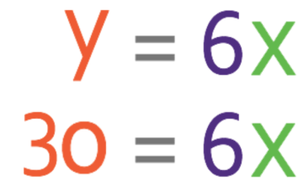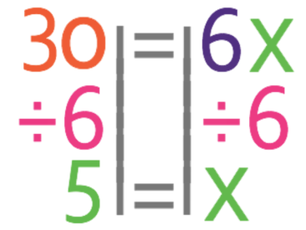Back to AQA Direct & Inverse Proportion (H) Home
3.1 D) Direct Proportion – Part 2
3.1 D) Direct Proportion – Part 2
From the previous sections, we learnt that variables that are in direct proportion move in the same direction as one another and by the same proportion. For example, if we had two variables that are in direct proportion (variable x and variable y), and variable x was to triple, variable y would also triple. Also, if variable x was to halve, variable y would also halve.
The notation for variables x and y being in direct proportion is:
The notation for variables x and y being in direct proportion is:
With the general equation:
k in the above equation is a constant (a number). We would be able to find the value of k if we were given a set of values for x and y. After we have found the value for k, we can sub in any value for x to find the corresponding value of y (or sub in any value for y to find the corresponding value for x).
I am now going to use the general equation for direct proportion to answer the second question in the previous section (click here if you would like to be taken back to the previous question). Here is a reminder of the previous question:
It costs £12 to purchase 2 footballs. How much would it cost to purchase 8 footballs?
The total cost of the footballs and the number of footballs will be in direct proportion to one another. I am going to let y be the total cost of the footballs and x be the number of footballs.
As these variables are in direct proportion, the notation would be:
I am now going to use the general equation for direct proportion to answer the second question in the previous section (click here if you would like to be taken back to the previous question). Here is a reminder of the previous question:
It costs £12 to purchase 2 footballs. How much would it cost to purchase 8 footballs?
The total cost of the footballs and the number of footballs will be in direct proportion to one another. I am going to let y be the total cost of the footballs and x be the number of footballs.
As these variables are in direct proportion, the notation would be:
We would then have the general equation:
We are able to find the value of k by subbing in a pair of values for x and y. The pair of values will come from the question and we were told in the question that it costs £12 to purchase 2 footballs. I let variable y be the total cost, which means that y will be 12. I let variable x be the number of footballs, which means that x will be 2. We sub these values into the general equation.
We want to find the value of k and not 2k. Therefore, we need to divide both sides of the equation by 2.
Therefore, k is 6.
The next step is to replace the k in the general equation for direct proportion (y = kx) with a 6. This gives us the equation:
The next step is to replace the k in the general equation for direct proportion (y = kx) with a 6. This gives us the equation:
We now have the general equation. This equation is useful because we can sub in any value for x or y to find the value of the other variable; we can sub in a value for x to find y, or we can sub in a value for y to find x.
The question asks us to find the total cost of purchasing 8 footballs. The variable y is the total cost and this is what we are looking for. The variable x is the number of footballs purchased, which means that x is 8. Therefore, we can find the value of y (the cost of purchasing 8 footballs) by subbing in x as 8 into the general equation with the value of k known.
The question asks us to find the total cost of purchasing 8 footballs. The variable y is the total cost and this is what we are looking for. The variable x is the number of footballs purchased, which means that x is 8. Therefore, we can find the value of y (the cost of purchasing 8 footballs) by subbing in x as 8 into the general equation with the value of k known.
This tells us that y is 48, which means that the total cost of purchasing 8 footballs is £48. This is exactly the same as we found with the unitary method that we used in the previous section.
Extension
Let’s now suppose that the question was extended. The total cost of the footballs is £30. How many footballs were purchased?
For the extension, we are finding the number of footballs that can be purchased, which is variable x. The question tells us that the total cost of the footballs is £30, which means that y is 30. We are able to find the value of x by subbing in y as 30 into the general equation with the value of k known.
Let’s now suppose that the question was extended. The total cost of the footballs is £30. How many footballs were purchased?
For the extension, we are finding the number of footballs that can be purchased, which is variable x. The question tells us that the total cost of the footballs is £30, which means that y is 30. We are able to find the value of x by subbing in y as 30 into the general equation with the value of k known.
We want to find the value of x and not the value of 6x. Therefore, we need to divide both sides of the equation by 6.
This tells us that x is 5, which means that we can buy 5 footballs for £30.
End Note
It is probably easier to answer this example by using the unitary method (the method that was used in the previous section). But you will need to answer most direct proportion questions by using the direct proportion framework (y = kx). Hopefully, the example that we have looked at has helped you to understand how the direct proportion framework works. In the next section, we are going to have a look at some more typical direct proportion questions.
It is probably easier to answer this example by using the unitary method (the method that was used in the previous section). But you will need to answer most direct proportion questions by using the direct proportion framework (y = kx). Hopefully, the example that we have looked at has helped you to understand how the direct proportion framework works. In the next section, we are going to have a look at some more typical direct proportion questions.