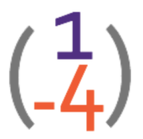Back to AQA Vectors (H) Home
4.12 A) Introduction
4.12 A) Introduction
There are two different measurements when we are looking at movement; these are scalar and vector quantities.
Vectors have both magnitude and direction. An example would be “an object travelling at 20 m/s in a northwards direction”. We know the magnitude of our object, which is 20 m/s, and we know the direction of our object, which is northwards.
Scalar quantities only have a magnitude; they have no direction. An example of a scalar quantity would be “an object travelling at 60 mph”. We have a magnitude from this statement because we are told that the object is travelling at 60 mph, but we do not have a direction; this individual could be going northwards, eastwards, up, down etc.
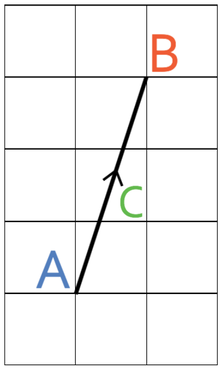
Here is an example of a vector.
Vectors have both magnitude and direction. An example would be “an object travelling at 20 m/s in a northwards direction”. We know the magnitude of our object, which is 20 m/s, and we know the direction of our object, which is northwards.
Scalar quantities only have a magnitude; they have no direction. An example of a scalar quantity would be “an object travelling at 60 mph”. We have a magnitude from this statement because we are told that the object is travelling at 60 mph, but we do not have a direction; this individual could be going northwards, eastwards, up, down etc.
Here is an example of a vector.
When we are working with vectors, we need to be very clear about what direction the vector is going in. We always place arrows to show the direction the vector is going in. The arrow for the vector above is pointing in an upwards rightwards direction, which means that the vector is going from point A to point B.
There is a few different ways that vectors can be written. We can write the vector above as:
There is a few different ways that vectors can be written. We can write the vector above as:
Column Vectors
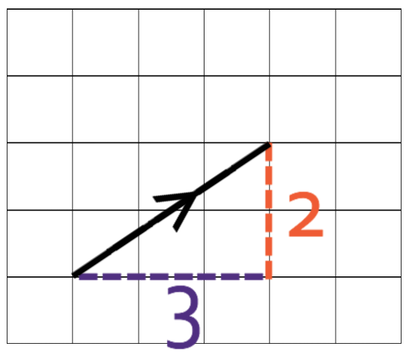
Column vectors are another way that vectors can be represented. At GCSE you are only required to know about two-dimensional column vectors. As there are 2 dimensions, the column vector will have 2 numbers; the top number is the displacement (movement) in the x direction and the bottom number in the displacement in the y direction.
Column vectors are another way that vectors can be represented. At GCSE you are only required to know about two-dimensional column vectors. As there are 2 dimensions, the column vector will have 2 numbers; the top number is the displacement (movement) in the x direction and the bottom number in the displacement in the y direction.
If the top number in the column (displacement in the x direction) is positive, the displacement is towards the right. If the top number is negative, the displacement is towards the left.
If the bottom number in the column vector (displacement in the y direction) is positive, the displacement is upwards. If the bottom number in the column vector is negative, the displacement is downwards.
Let’s have a few questions about column vectors.
Question
Draw the following column vectors.
Vector A
If the bottom number in the column vector (displacement in the y direction) is positive, the displacement is upwards. If the bottom number in the column vector is negative, the displacement is downwards.
Let’s have a few questions about column vectors.
Question
Draw the following column vectors.
Vector A
The top number in column vector A is 3, which means that it is moving 3 to the right. The bottom number in the column vector is 2, which means that it is moving 2 up. Therefore, the vector A is moving 3 to the right and 2 up. We need to make sure that we include our arrow on our vector. The arrow will be pointing in the direction from where we started from to where we end up (it will roughly be in a north east direction). The vector diagram is shown below.
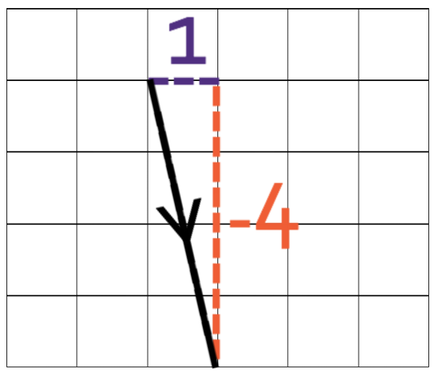
Vector B
The top number of column vector B is 1, which means that we are moving 1 towards the right. The bottom number in the column vectors is -4, which means that the vector is moving 4 down. Therefore, vector b moves 1 to the right and 4 down. We need to put an arrow indicating the direction of the vector. The vector diagram is shown below.
Question
Place the following vectors into column vector form.
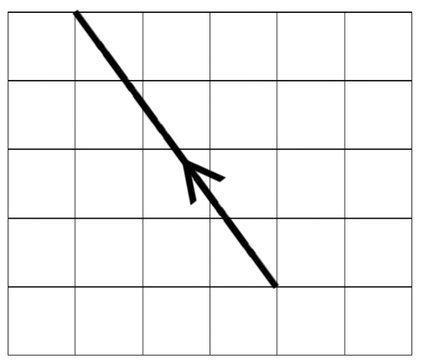
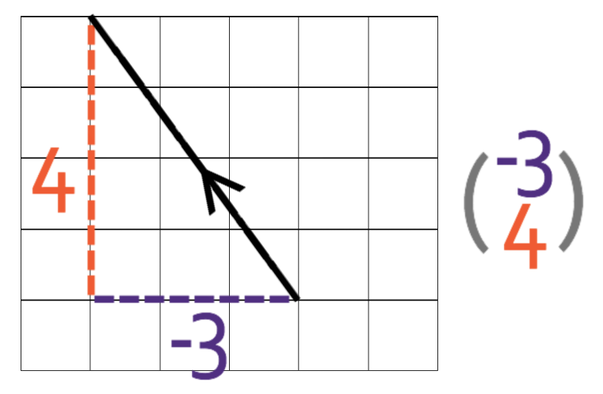
Vector C
Place the following vectors into column vector form.
Vector C
Vector C moves 3 to the left and 4 upwards. The top component of the column vector shows us the displacement in the x direction where positive values mean that the displacement is towards the right and negative values meaning that the displacement is towards the left. The displacement for vector C is 3 in a leftwards direction and this means that the value for the top component is -3. The bottom component in a column vector is the displacement in the up and down direction. A positive value for this component means that the displacement is in an upwards direction and a negative value means that the displacement is in a downwards direction. Vector C is moving 4 up and this means that the bottom component of our column vector is 4. Therefore, the column vector for C is:
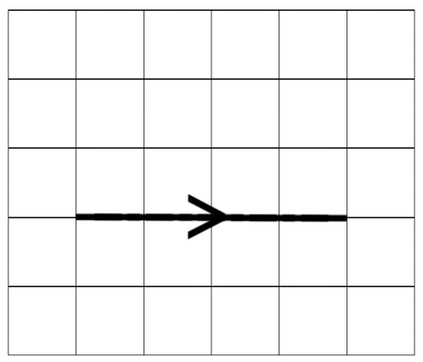
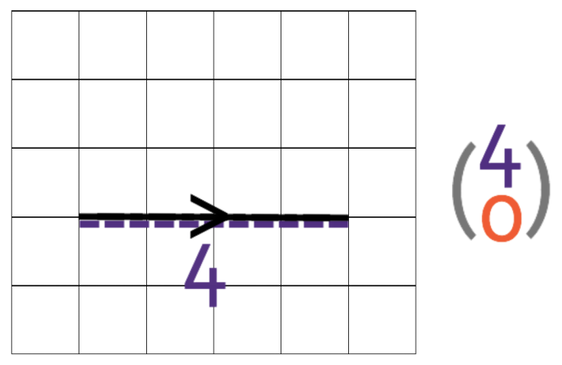
Vector D
Vector D moves 4 towards the right and there is no movement in an upwards or downwards direction. As it is moving 4 to the right, the value for the top component is 4. There is no movement up or down and this means that the bottom component in the column vector is 0. The column vector for D is: