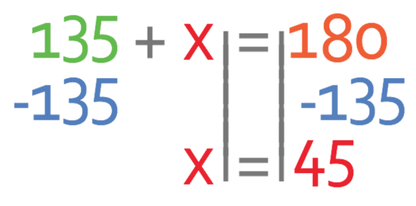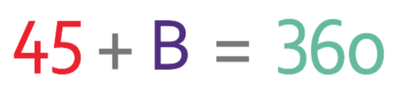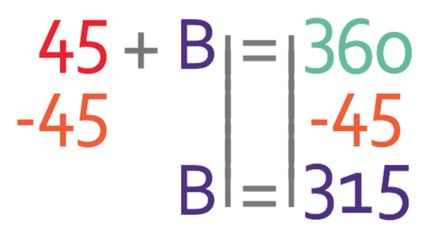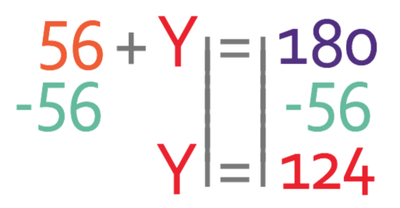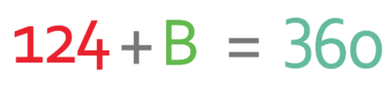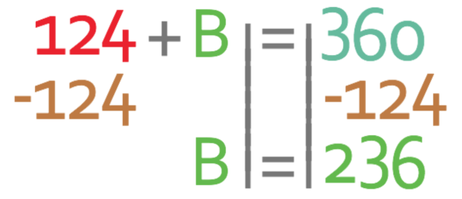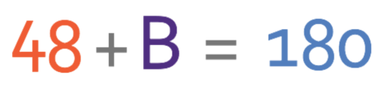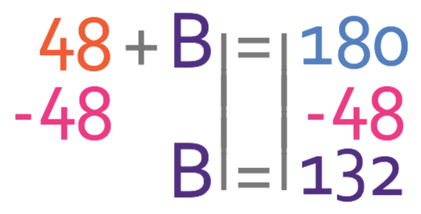Back to AQA Loci & Construction (H) Home
4.2 H) Bearings – Part 2
4.2 H) Bearings – Part 2
The content in this section builds on the content that was discussed in the previous section. Make sure that you have covered the content in the previous section before working through the content in this section (click here to be taken to the content in the previous section).
Bearing Main Rules
From the previous section we learnt that there are 3 key rules that we need to remember with bearings. These rules are shown below:
Let’s now have some more complex examples.
From the previous section we learnt that there are 3 key rules that we need to remember with bearings. These rules are shown below:
- They are measured from the North line
- They are measured in a clockwise direction
- They are measured in degrees and we always give them as 3 digits
Let’s now have some more complex examples.
Example 1
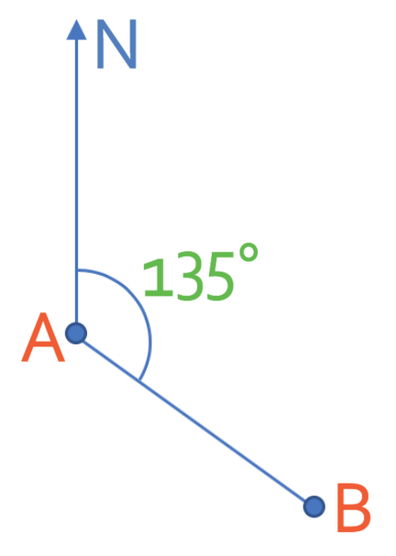
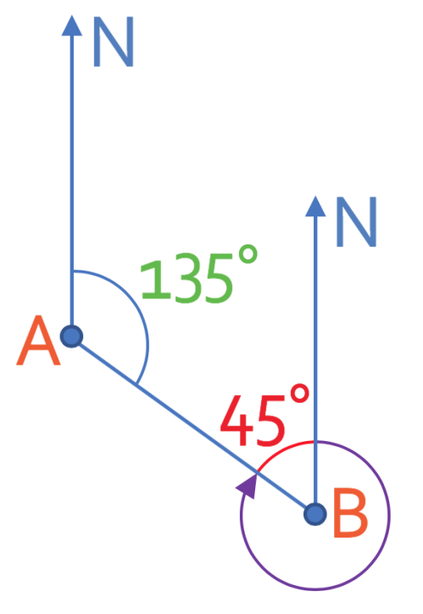
The bearing of B from A is 135°. What is the bearing of A from B? The sketch below is not drawn to scale. Click here for a printable version.
The bearing of B from A is 135°. What is the bearing of A from B? The sketch below is not drawn to scale. Click here for a printable version.
We need to be really careful when we are answering questions like this and this is because the process to get to the answer is more complex than people expect.
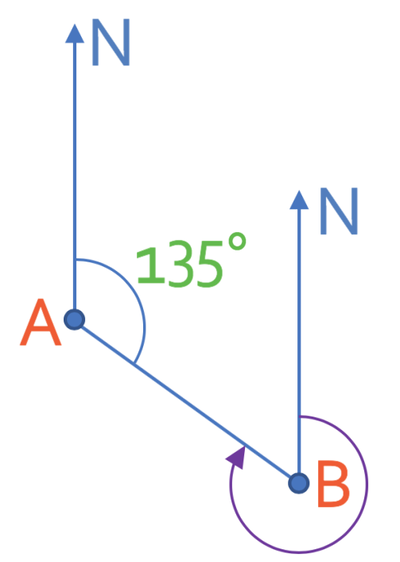
We know that bearings are always measured clockwise from the north line. Therefore, the first step in answering this question is to draw a north line for point B.
We know that bearings are always measured clockwise from the north line. Therefore, the first step in answering this question is to draw a north line for point B.
The curved purple arrow on the above diagram is the bearing that we are looking for.
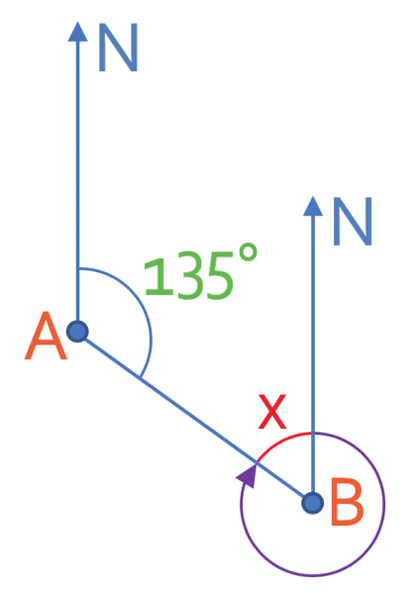
On the above diagram, we now have two north lines and these two lines will be parallel to one another. From the section on parallel lines, we know that the two angles inside parallel lines add up to 180°. This means that the angle that is 135° and the angle that is labelled x on the diagram below add up to 180°.
On the above diagram, we now have two north lines and these two lines will be parallel to one another. From the section on parallel lines, we know that the two angles inside parallel lines add up to 180°. This means that the angle that is 135° and the angle that is labelled x on the diagram below add up to 180°.
We are able to create the following equation from these two angles.
We want to find the values of x and we are able to do this by moving the 135 from the left side of the equation to the right. We move the 135 by doing the opposite; we take 135 from both sides of the equation.
Therefore, x is 45° and I have labelled this angle on the diagram below.
We are now in a position to find the size of the bearing. A full circle is 360°. This means that the bearing that we are looking for and the 45° angle will add up to 360°. We are able to create the following equation form this information; B in the equation below stands for the bearing that we are looking for.
We are able to find the value of B by moving the 45 from the left sides of the equation to the right. We move the 45 by doing the opposite; we take 45 from both sides of the equation.
Therefore, the bearing of A from B is 315°.
Example 2
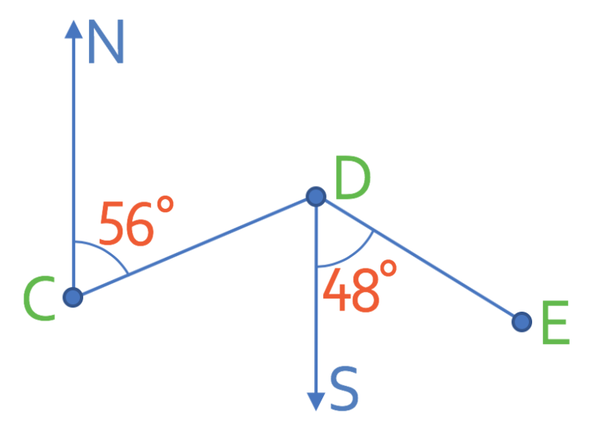
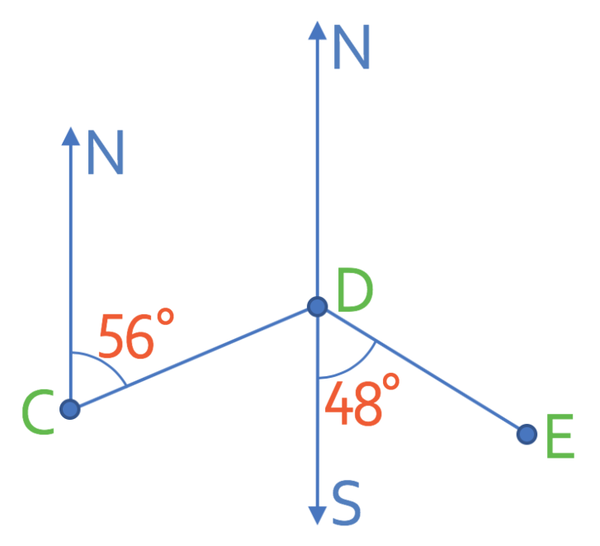
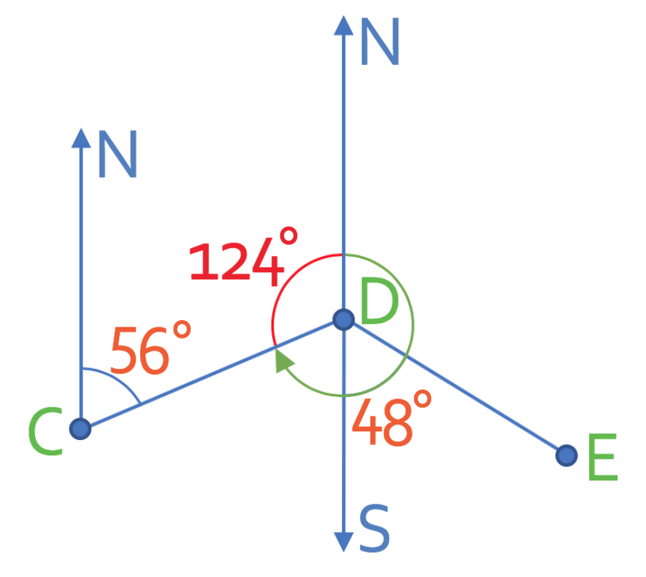
There are 3 different points on the diagram below; point C, D and E.
There are 3 different points on the diagram below; point C, D and E.
Answer the following:
Part 1
The first part of this question is asking us to find the bearing of C from D. We answer this question in a very similar way to the previous question. The first step is to draw in a north line from D.
- Find the bearing of C from D
- Find the bearing of E from D
Part 1
The first part of this question is asking us to find the bearing of C from D. We answer this question in a very similar way to the previous question. The first step is to draw in a north line from D.
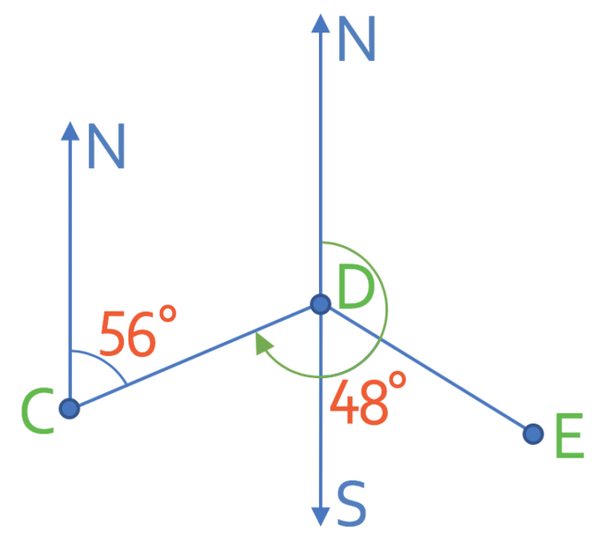
We always measure bearing clockwise from the north line. The bearing that we are looking for is shown on the diagram below (it is the green arrow).
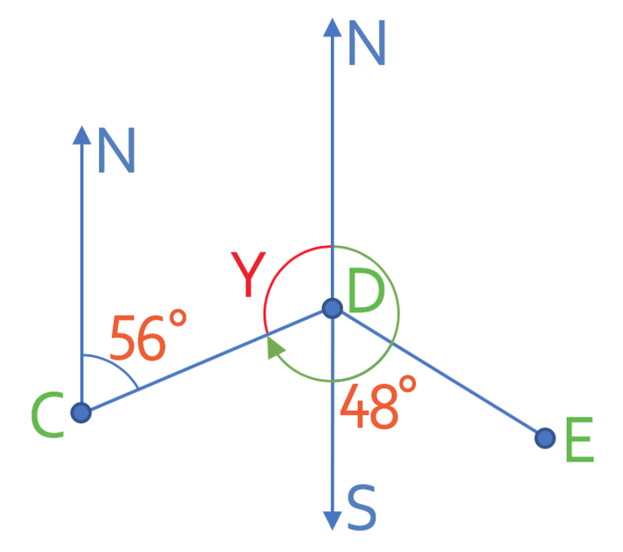
We are able to find this bearing by finding the size of the angle that goes from the end of the bearing to the north line. I have labelled this angle y on the diagram below.
We can find the value of y by using the two parallel north lines. We know that angles inside parallel lines add up to 180°. We can create the following equation from this information.
We want to find the value of y, which we do by moving the 56 from the left to the right. We are able to do this by taking 56 from both sides of the equation.
y is 124°. I have added this angle to the diagram below.
We know that the bearing that we are looking for and the angle that we have just found will add up to 360°. Therefore, we can create the following equation (B in the equation below is the bearing that we are looking for):
We are able to find the value of B by taking 124 from both sides of the equation.
The bearing of C from D is 236°.
Part 2
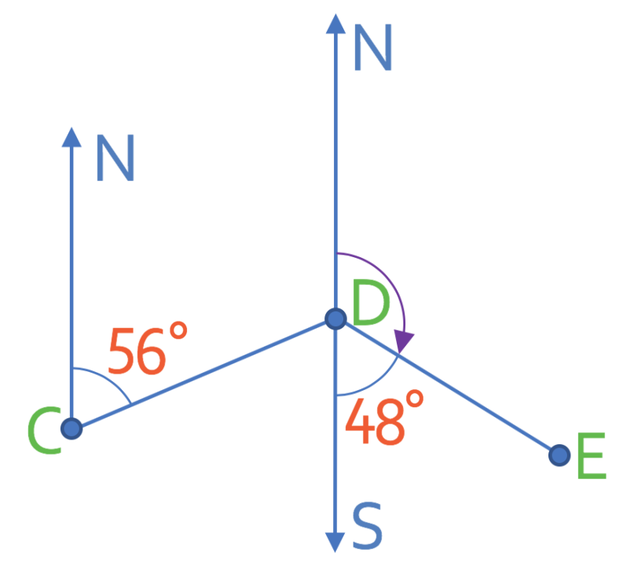
The second part asks us to find the bearing of E from D. The bearing that we are looking for is shown on the diagram below.
Part 2
The second part asks us to find the bearing of E from D. The bearing that we are looking for is shown on the diagram below.
On the above diagram we are given a south line. The south line will have a bearing of 180°. There are two angle that make up the south line bearing; these angles are the bearing that we are looking for in this question (the bearing of E from D) and the angle that we are given in the diagram (the angle that is 48°). Therefore, we can create the following equation from this information (I am going to let the bearing that we are looking for equal B):
We want to find the value of B, and we do this by taking 48 from both sides of the equation.
Therefore, the bearing of E from D is 132°.