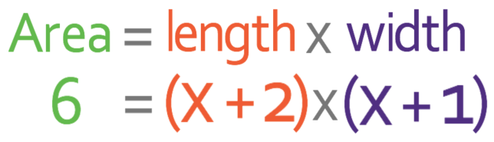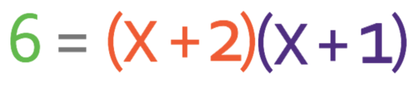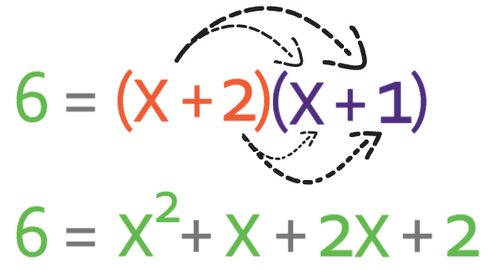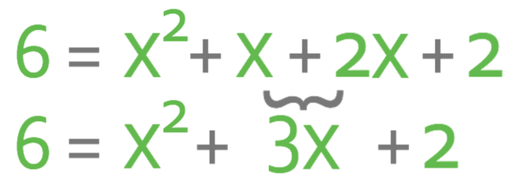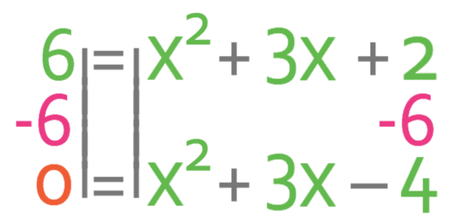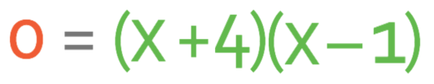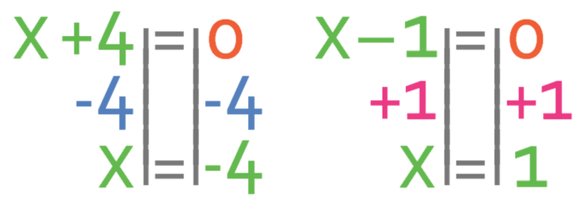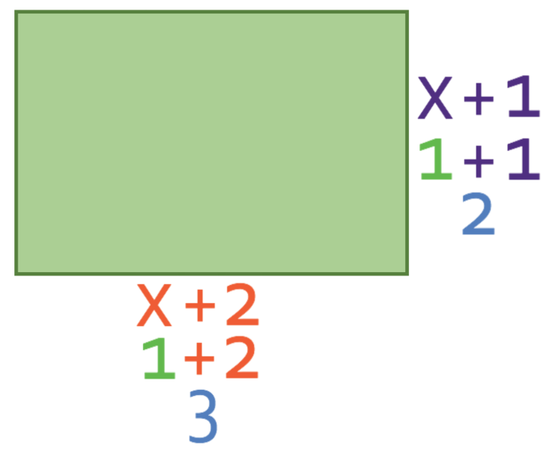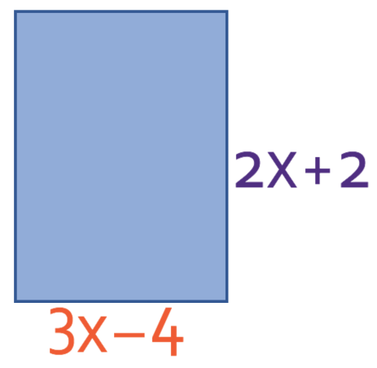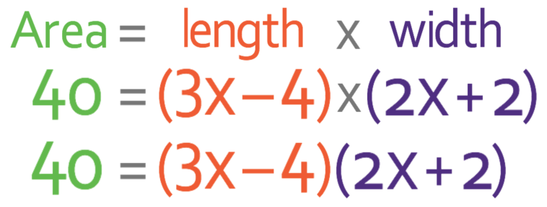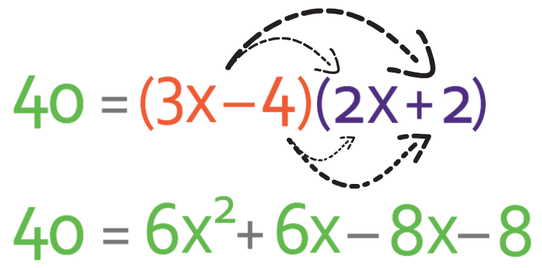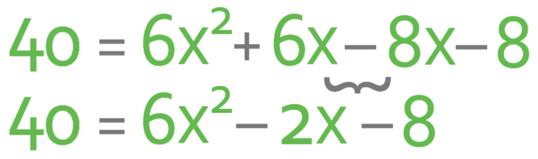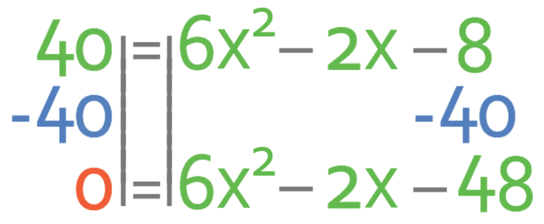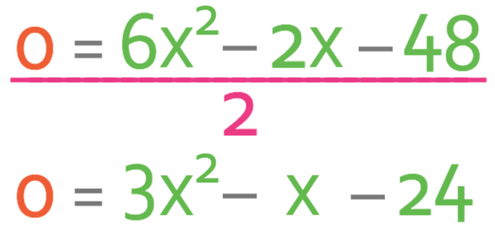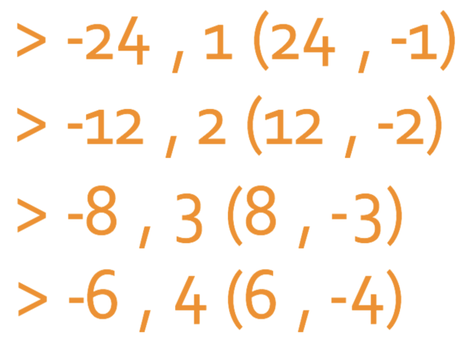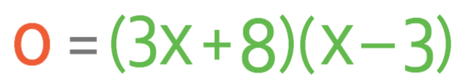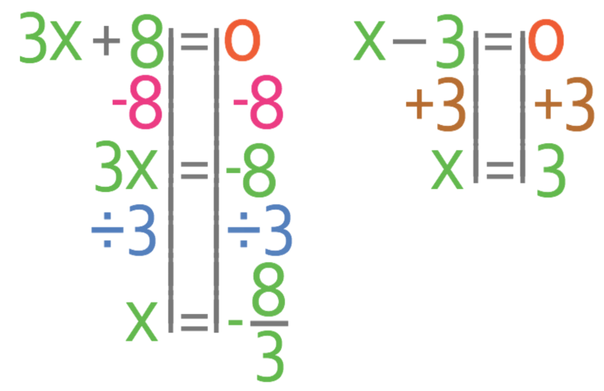Back to AQA 2D Shapes (H) Home
4.5 F) Area of Rectangles – Part 3
The content in this section builds on the content that was discussed in the previous section. Make sure that you have covered the content in the previous section before working through the content in this section (click here to be taken to the previous section)
Example 1 
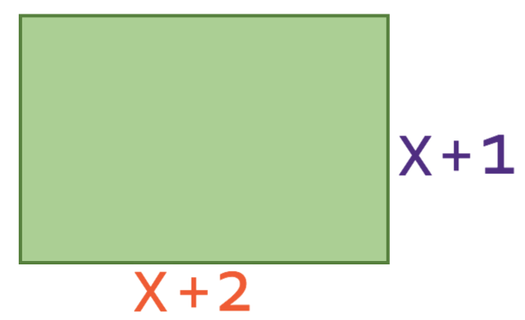
The rectangle below has an area of 6 square units. Find the value of x. 
We are going to find the value of x by creating an equation. We are told in the question that the area of the rectangle is 6 square units. Also, we know that we are able to work out the area of the rectangle by multiplying the length of the rectangle by the width. This means that we can create the following equation. 
Like the examples in the previous section, I am going to tidy this equation up by getting rid of the multiply sign between the two brackets. 
We are now ready to multiply out the brackets on the right side of the equation. Each of the brackets contain two terms, and one way to multiply out these brackets is to use the FOIL method (First, Outside, Inside and last). The working is shown below. 
The next step is to collect any like terms. There are two terms on the right side of the equation that just contain an x; x and 2x. We are able to combine these terms together. 

We want to solve to find the value of x and we do this by getting all of the terms to one side of the equation and having the other side of the equation as 0. It is best to have a positive number of x2 terms. Therefore, I am going to get all of the terms on the right side of the equation and I will have the left side of the equation as 0. This means that I need to move the 6 that is currently on the left side to the right. I am able to move the 6 from the left to the right by doing the opposite; I take 6 from both sides of the equation.

The next step is to solve the quadratic equation, which we do by factorising. Our quadratic equation is in the form of ax2 + bx + c, where the value of a is 1, b is 3 and c is -4. As the value for a is 1, we are looking for two terms that multiply together to give -4 (the value of c) and add together to give 3 (the value of b). The two numbers that we are looking for are 4 and -1. Therefore, the factorised equation becomes.

We can find the values of x by letting each of the brackets equal 0. This is because in order for the equation to be 0, one of the brackets must be 0. The working is shown below. 
​The value for x cannot be -4 because this would give us a negative length and a negative width. Therefore, the only possible value of x is 1.
 
This means that the length of the rectangle is 3 and the width is 2. When we multiply these together to find the area, we get 6, thus showing that we have found the correct value for x; x is 1. 
Picture
The lengths of each side are shown in blue.
Example 2 
The area of the shape below is 40 units squared. What is the value of x and what are the length and width of the rectangle below?
We are told in the question that the area of the rectangle is 40 square units. We also know that the area of a rectangle is worked out by multiplying the length by the width. The length of our rectangle is 3x – 4 and the width is 2x + 2. We are able to create the following equation from this information.  
We now want to multiply out the brackets, which I am going to do by using the FOIL method (First, Outside, Inside and Last). 
​We are able to simplify the right side of the equation because there are two terms that contain x terms. This results in the equation becoming.
​We want to solve the equation and we do this by getting all of the terms to one side of the equation. It is easier to work with positive quadratic terms. Therefore, I am going to get all of the terms to the right side of the equation. This means that I need to move the 40 that is currently on the left to the right, and we can able to do this by doing the opposite; we take 40 from both sides of the equation.
The next step is to factorise our equation. But, before we factorise, we should check whether there is a common factor between all of the terms. If there is a common factor, we can divide all of the terms by this factor. When we look at the equation that we are trying to factorise, we see that 2 is a factor of all of the terms, so let’s divide every term by 2.
We are now factoring the equation. The value for a for this quadratic is not 1 (it is 3). This means that we are unable to factorise in the usual way (two numbers that multiply to obtain the value of c and add to give the value of b).
 
There are a few different methods that you can use to factorise this equation. I think the best method is write out the pair of numbers that give you -24, which are:

We want to get 3x2 when we multiply the first term in each of the brackets together. As 3 is prime, the only way that we are able to obtain 3x2 from two terms that contain x is to have 3x in one bracket and x in the other bracket. This means that the brackets start off like:

The next step is to play around with the pairs of numbers that when multiplied together give you -24 to see if you can obtain the equation that we are trying to factorise. The only pair of numbers that works for this equation are 8 in the first bracket and -3 in the second bracket.
​We now have the factorised equation and are able to find what the value of x is by setting each of these brackets equal to 0. We set the brackets equal to zero because if the multiplication of these brackets gives you zero, one of the brackets must be zero.

The value for x must be 3 and this is because if the values of x was -8/3, the length of the rectangle would be negative and we know that we cannot have a negative length (3 x (-8/3) – 4 = -8 – 4 = -12; we cannot have a length of -12). Therefore, x must equal 3.

 

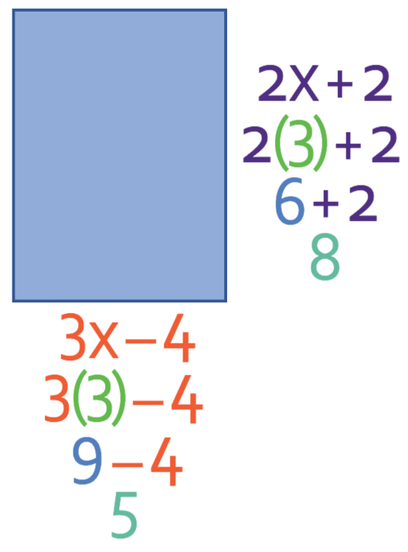
The final part of the questions asks us to find the length and the width of the rectangle. We can do this by subbing the value for x into the expressions for the length and the width. The working is shown below:

​Therefore, the length of the rectangle is 5 and the width of the rectangle is 8. We can check that we have found the correct answer by multiplying the length by the width to see if we obtain 40, which is exactly what we do obtain (5 x 8 = 40).