Back to AQA 2D Shapes (H) Home
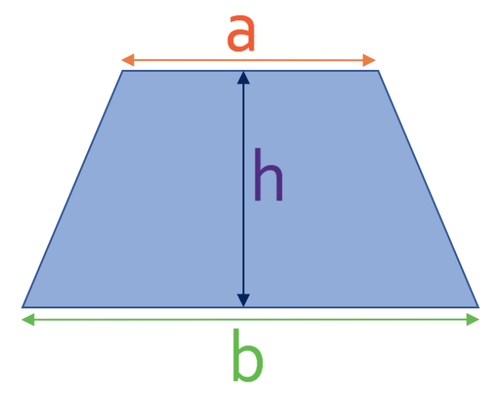
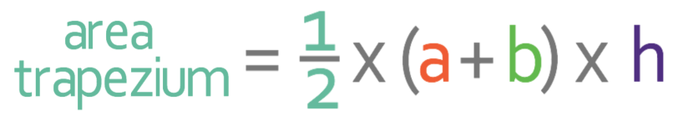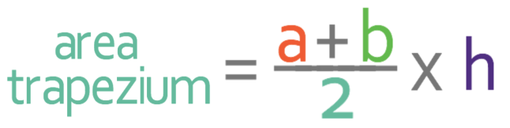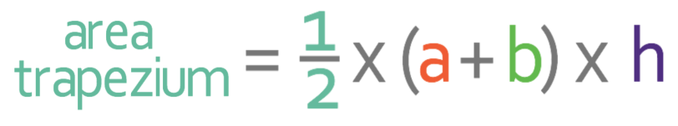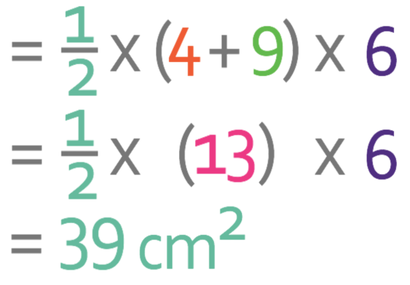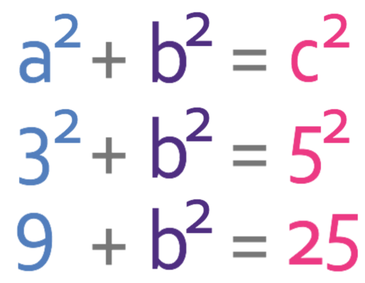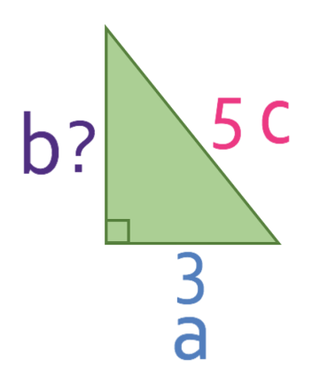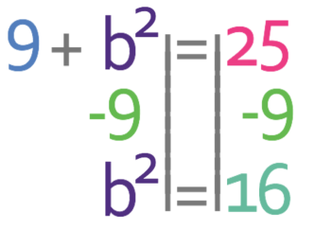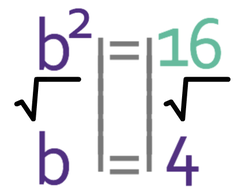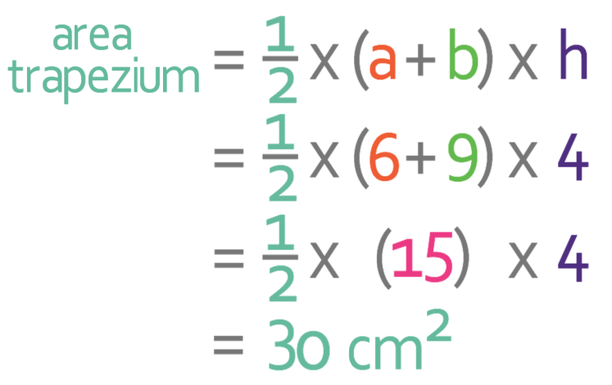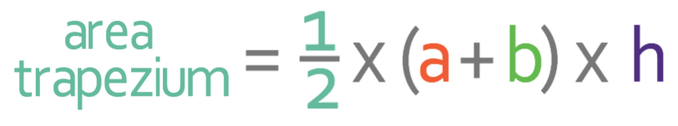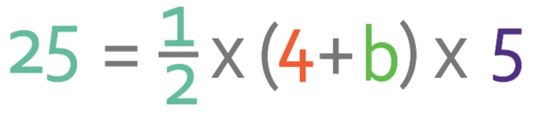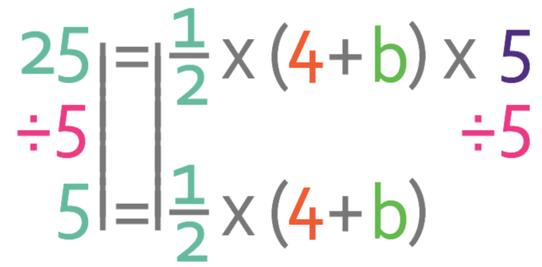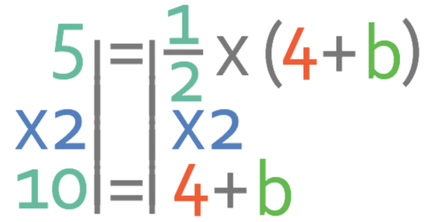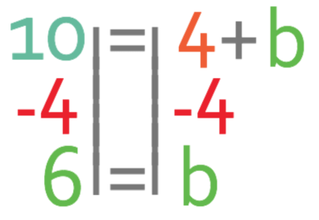4.5 M) Area of Trapeziums
A trapezium is a quadrilateral with one pair of parallel sides. 
We are able to work out the area of a trapezium by using the following formula.
​Where:
  • a and b are the two parallel sides
  • h is the perpendicular height; the distance between the two parallel sides
 
This formula can also be written as:
Let’s have an example.
Example 1 
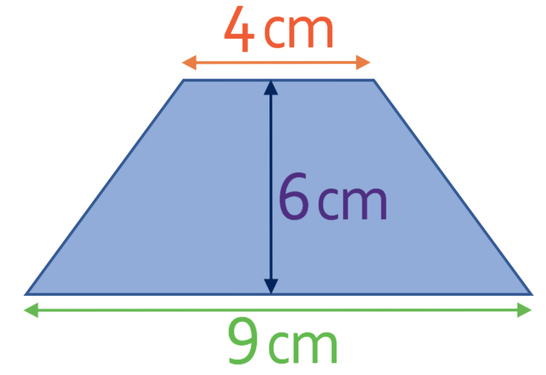
What is the area of the following trapezium?
 The formula for the area of a trapezium is given below.
a and b are the values for the lengths of the two parallel sides; it does not matter which side is which value. In the example above, the top of our trapezium is 4 cm and the bottom of our trapezium is 9 cm. I am going to have a as 4 cm and b as 9 cm. The diagram also gives us the perpendicular height of the trapezium, which is 6 cm. We are now able to sub these values into our formula. 

The area of the trapezium in the example is 39 cm2. 

Example 2 
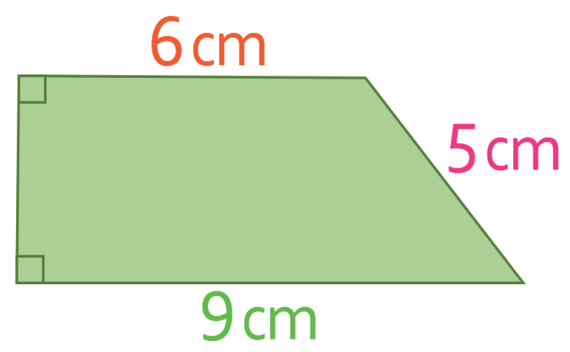
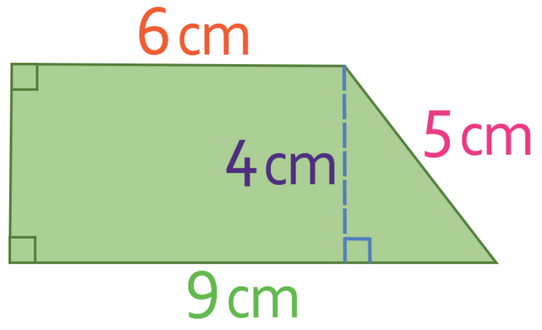
What is the area of the following trapezium?
In order to work out the area of a trapezium, we need to know what the lengths of the two parallel sides are (the values of a and b), and we are given these two values. Also, we need to know what the perpendicular height is, which we are currently not given. However, we are able to find the perpendicular height by creating a right-angled triangle. We can then use Pythagoras’ theorem to find the perpendicular height. The diagram below shows the right-angled triangle on the trapezium. 
We are already given the value for the hypotenuse of our right-angled triangle; the hypotenuse is 5 cm. We are not given the value of the two other sides of the triangle. However, we are able to work out the length of the bottom side by using the values that we are given for the base and the top of our trapezium. We can see that the base of our trapezium is 9 cm and the top of the trapezium is 6 cm. The difference between these two lengths is going to be the length of the bottom of our triangle and this is because both the top and the bottom create right-angles to the left side. Therefore, the base of our triangle is 3 cm (9 – 6).
 
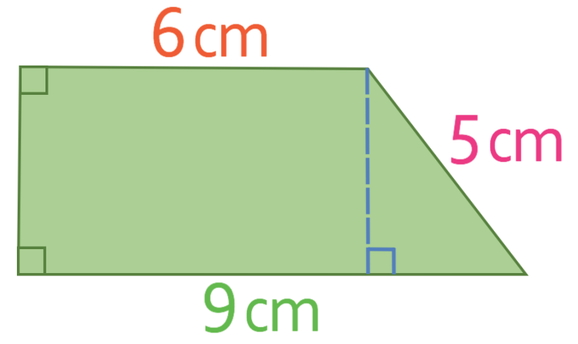
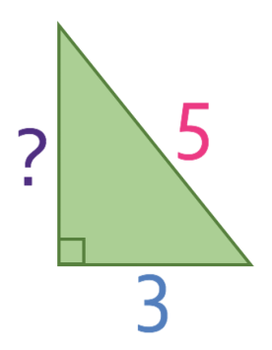
We now have two sides in our right-angled triangle, which means that we can use Pythagoras’ theorem to work out the other side (which is the perpendicular height of the trapezium). 
Pythagoras’ theorem states that the square of the hypotenuse is equal to the sum of the squares of the other two sides. His formula is shown below:
In the above formula, the hypotenuse is c and the other two sides are a and b. For the other two sides, it does not matter which side is which; I am going to let a be 3 and b be the perpendicular height that we are looking for. The hypotenuse for our right-angle triangle is 5. We can now sub these values in. 
The next step is to get the unknown by itself. This means that we need to move the 9 that is currently on the left to the right, and we do this by doing the opposite; we take 9 from both sides of the equation. 

We want to find the value of b and not b2. Therefore, we square root both sides of the equation.

Therefore, the perpendicular height of the trapezium is 4 cm. Let’s add this to the diagram.

We are now able to calculate the area of the trapezium by subbing the values into the area of a trapezium formula.

The area of the trapezium in the question is 30 cm2.

Example 3

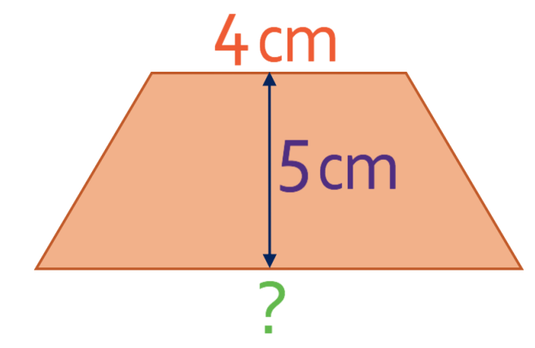
The area of the trapezium below is 25 cm2. What is the length of the base of the trapezium?

We are asked to work out the length of the base of this trapezium. The area of a trapezium formula has 4 different values; the area, the perpendicular height and the length of the two parallel sides. We are given all of the values in the question, except 1 (the base), which means that we can use the area of a trapezium formula to obtain the length of the base. Let’s let the base of the triangle equal b in the area of the trapezium formula.

The next step is to sub all of the values that we are given in the question.

There are a few different methods that we can use to find the value of b. The way that I would find the value of b is to deal with the multiply by 5 on the right sides of the equation first. We can get rid of the multiply by 5 on the right side of the equation by doing the opposite; we divide both sides of the equation by 5.

The next step is to get rid of the fraction. We are able to get rid of fractions by multiplying both sides of the equation by the denominator of the fraction. The denominator of the fraction is 2, so we multiply both sides by 2.

We now need to move the 4 from the left to the right, which we do by taking 4 from both sides of the equation.

Therefore, the base of the trapezium is 6 cm. You could check your answer by subbing b as 6 back into the formula for working out the area of a trapezium to see if you do get an area of 25 cm2.