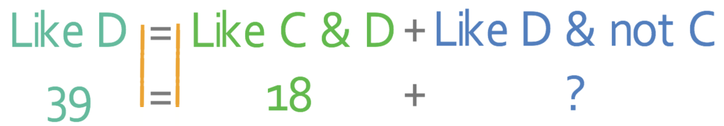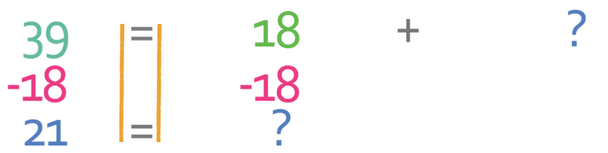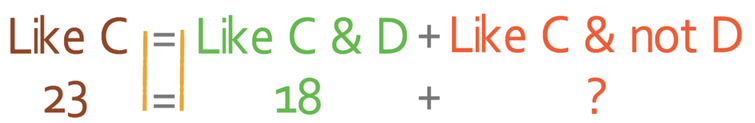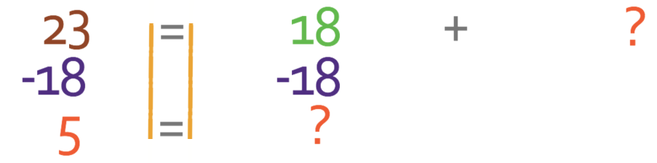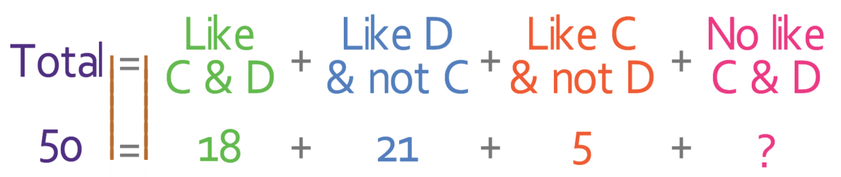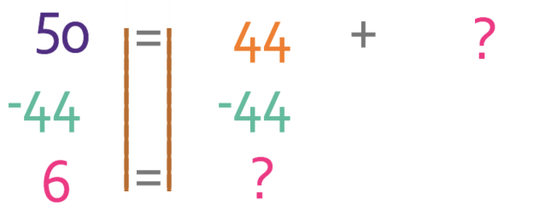Back to AQA Probability (H) Home
5 S) Venn Diagrams – Part 2
5 S) Venn Diagrams – Part 2
Usually in an exam you will be asked to fill in a Venn diagram from numbers/ information that you have been given. We are going to be looking at a question like this in this section.
Example 1
I ask a group of 50 individuals whether they like cats or dogs. These were the outcomes:
Fill in the Venn diagram below.
I ask a group of 50 individuals whether they like cats or dogs. These were the outcomes:
- 18 people like cats and dogs
- 39 people like dogs
- 23 like cats
Fill in the Venn diagram below.
The circle on the left indicates that an individual likes dogs; being inside this circle means that you like dogs and being outside this circle means that you do not like dogs.
The circle on the right indicates that an individual likes cats; being inside this circle means that you like cats and being outside the circle means that you do not like cats.
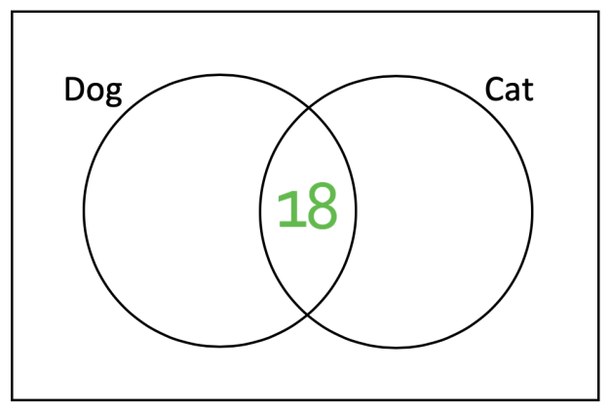
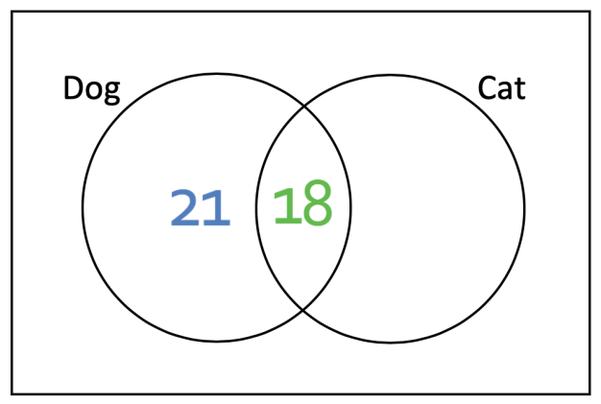
The part where both of the circles cross is where an individual is in both of the circles and this means that they like both dogs and cats. We are told in the question that 18 people like cats and dogs, which means that we can put 18 into the centre of the Venn diagram.
The circle on the right indicates that an individual likes cats; being inside this circle means that you like cats and being outside the circle means that you do not like cats.
The part where both of the circles cross is where an individual is in both of the circles and this means that they like both dogs and cats. We are told in the question that 18 people like cats and dogs, which means that we can put 18 into the centre of the Venn diagram.
Let’s now deal with the area that is on the left of the diagram, which represents individuals that like dogs and do not like cats. We are not given the number of individuals that like dog and not cats in the question, but we are able to work this figure out from the information that we have been given. We are told in the question that 39 people like dogs. This number represents the number of individuals that appear inside the “like dogs” circle. The “like dog” circle is made up of the middle section (where people like dogs and cats) and the other part that we are trying to find (like dogs and do not like cats). This means that we have the following equation.
We can sub the appropriate numbers into the above equation to find the number of individuals that like dogs and do not like cats.
The next step is to move the 18 from the left side of the equation to the right. We are able to do this by taking 18 from both sides of the equation.
Therefore, we can see that 21 people like dogs and do not like cats.
We are able to use pretty much the same method to find the number of individuals that appear on the right part of the diagram. These individuals are inside the “like cat” and outside the “like dog” circle, which means that individuals in this area like cats and do not like dogs. We can find the number of individuals in this category by using the following equation.
We can sub the numbers into the equation.
Like with the previous equation, we need to move the 18 from the left side of the equation to the right. We are able to do this by taking 18 from both sides of the equation.
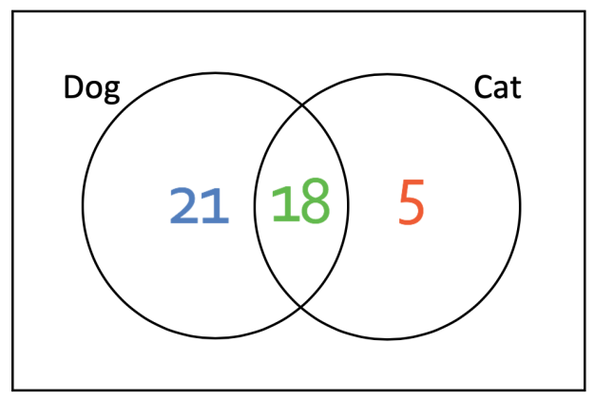
We can therefore see that 5 individuals like cats and not dogs.
There is one more part to work out on the diagram and this is the outside part of the diagram. This part of the diagram is outside both of the circles, which means that individuals in this area do not like dogs and do not like cats. We are told in the question that 50 people are asked whether they like cats and dogs, and we know that these 50 people must go into the four different parts of the diagram (the four parts of the diagram must add up to 50). We have worked out 3 parts of the diagram and have the total number of individuals that were asked, which means that we can find the number of individuals that do not like dogs and do not like cats by using the equation below.
We can now sub the values in.
The next step is to collect all of the numbers on the right side of the equation.
We now need to move the 44 that is currently on the right to the left. We do this by taking 44 from both sides of the equation.
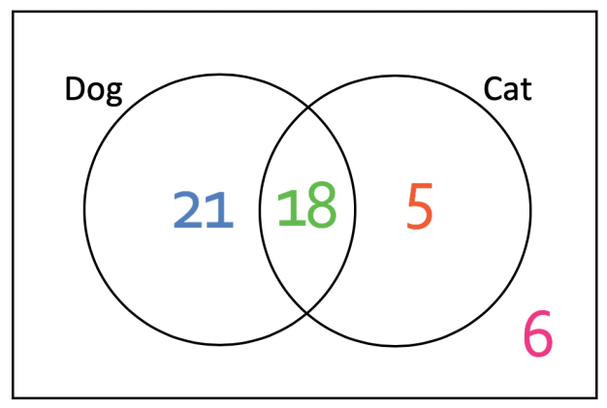
Therefore, 6 people do not like cats and dogs. The completed Venn diagram is given below.