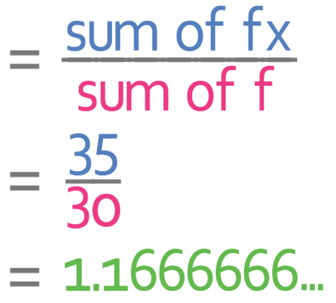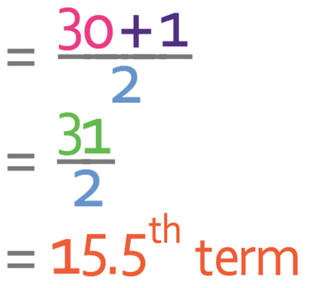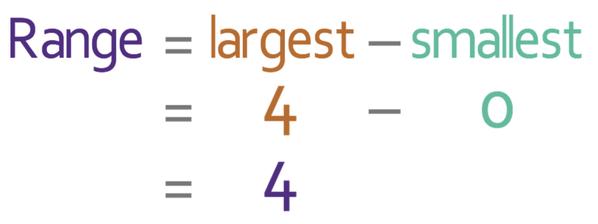Often a frequency table will be used when there is a vast quantity of data. We are still able to work out the mean, mode, median and range for the data, but the process is slightly different. Let’s have an example.
Example
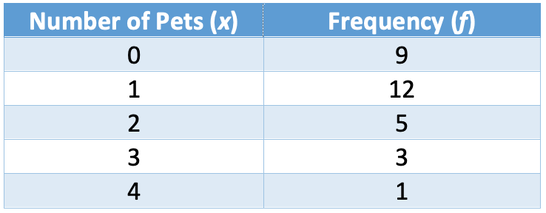
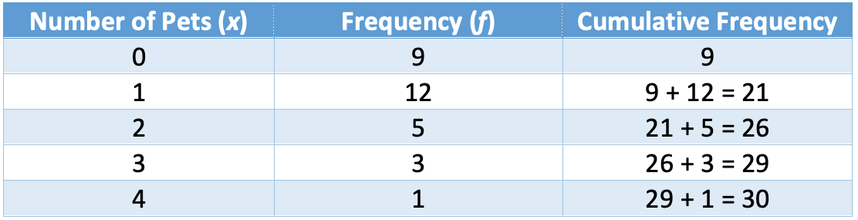
The frequency table below shows the number of pets that the 30 members of a class have. No one in the class has more than 4 pets.
The frequency table below shows the number of pets that the 30 members of a class have. No one in the class has more than 4 pets.
What is the mean, mode, median and range for this data? Give your answers to one decimal place.
Mean
We work out the mean of the data by adding up all of the values in the data and dividing this number by the amount of values that there were in the data set. The formula is shown below:
Mean
We work out the mean of the data by adding up all of the values in the data and dividing this number by the amount of values that there were in the data set. The formula is shown below:
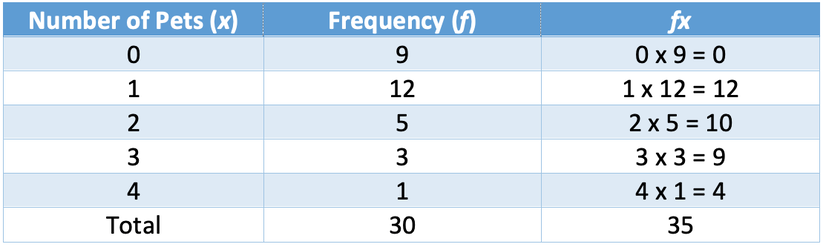
To assist us in adding all of the data together, we add another column that is titled fx. We obtain the values in this column by multiplying the number of pets (x) by the frequency (f). Also, we add a total row at the bottom of the table that works out the amount of values in the data set (sum of the frequencies) and the total number of pets that our class had (the sum of fx’s). The completed table is shown below.
We are now able to find the mean by using the mean formula.
We now need to round to one decimal place.
Therefore, the mean number of pets is 1.2.
Mode
Let’s now find the mode. The mode is the most common value and the most common number of pets in the data above is 1 pet (12 people have 1 pet).
Median
The median is the middle value in the ordered data set. We are able to find which term the middle value is in the ordered data set by using the formula below.
Mode
Let’s now find the mode. The mode is the most common value and the most common number of pets in the data above is 1 pet (12 people have 1 pet).
Median
The median is the middle value in the ordered data set. We are able to find which term the middle value is in the ordered data set by using the formula below.
n in the formula above stands for the amount of values that are in the data set. There are 30 values/ children, so we sub in n as 30 into the above equation.
The median term will be the 15.5th term in the ordered data set. To assist us in finding this term, we can add an additional column called cumulative frequency. Cumulative frequency is the sum of the frequencies for the class and all of the other classes below it in a frequency distribution. The working is shown in the table below.
The addition of the cumulative frequency column makes it easier to see where the 15.5th term is. The second group is the table (1 pets) starts with the 10th term and ends with the 21st term. This means that the 15.5th term will appear in this group. Therefore, the median for the above data is 1 pet.
Range
We now only need to work out the range, which we do by taking the smallest value away from the largest value. The smallest number of pets is 0 and the largest number of pets is 4. We sub these values into the formula.
The range is 4.
Here is a summary of the averages that we found for the data:
Here is a summary of the averages that we found for the data:
- Mean: 1.2
- Mode: 1
- Median: 1
- Range: 4