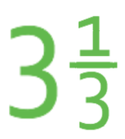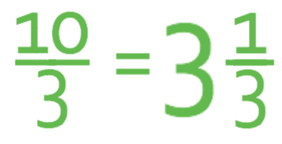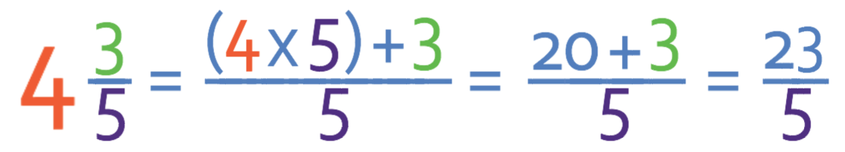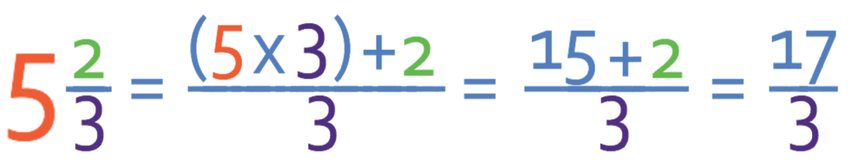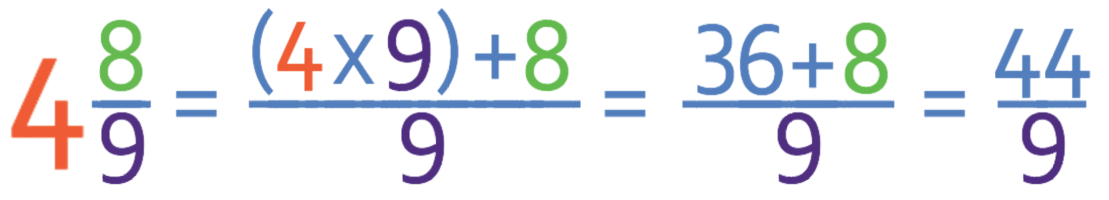1.3 E) Mixed Numbers & Improper Fractions – Part 1
A mixed number is a whole number and a fraction written together. An example of a mixed number is:
The two examples that I use above are equal to one another:
We convert a mixed number into an improper fraction by:
- Multiplying the whole number by the denominator
- Adding this number on to the numerator
Convert the mixed number below into an improper fraction.
The first step is to multiply the whole number (4) by denominator of the fraction (5). This gives us 20 (4 x 5 = 20).
The final step is to add the numerator (3) onto the value that we have found (20). This means that the numerator for the improper fraction is 23 (20 + 3). The denominator of the improper fraction remains the same. Therefore, the improper fraction is 23/5.
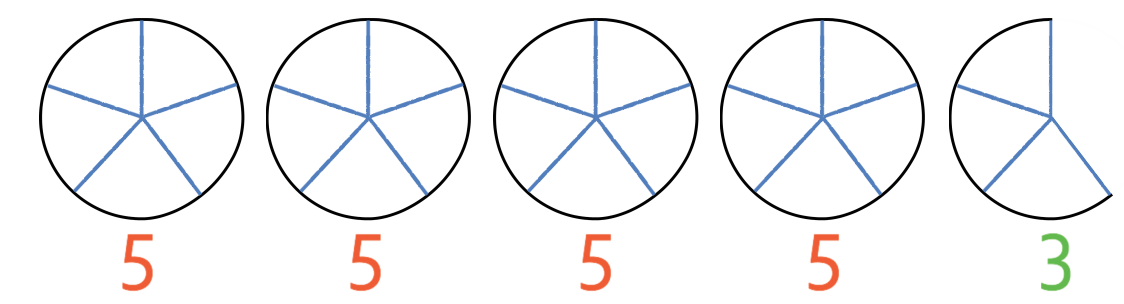
Another way to see how we convert a mixed number into an improper fraction is to draw the wholes and fraction out. One circle represents a whole.
We have 4 wholes, and each whole is made up of 5 one fifths. This means that the four whole circles are made up of 20 fifths. In addition to our four wholes, we also have 3 additional fifths. Therefore, in total we have 23 fifths, which can be written in fraction form as 23/5.
Convert the mixed number below into an improper fraction.
The first step is to multiply the whole number (5) by the denominator of the fraction (3). Therefore, 5 wholes in terms of thirds is 15 thirds (5 x 3).
The next step is to add this number (15) to the numerator of the original fraction (2). This means that in total, we have 17 thirds, which we can be written as 17/3.
Convert the mixed number below into an improper fraction.
Like the previous two examples, the first step is to multiply the whole number (4) by the denominator of the fraction (9). Therefore, 4 wholes in terms of ninths in 36 ninths (4 x 9).
The next step is to add this number (36) to the numerator of the fraction (8). Therefore, in total there are 44 ninths (36 + 8) and the improper fraction is 44/9.