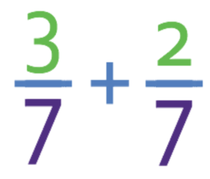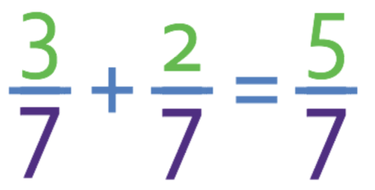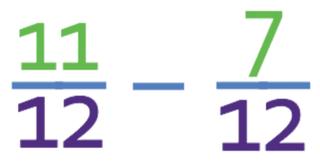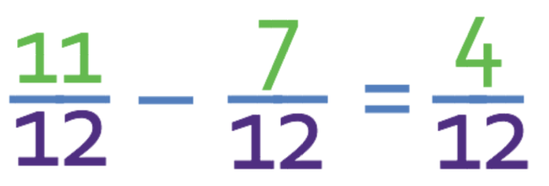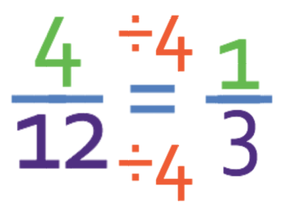1.3 G) Adding & Subtracting Fractions – Part 1
If the denominators of the fractions are not the same, we can create equivalent fractions to the fractions that are in the question with a common denominator.
The examples in this section will look at adding or subtracting fractions whereby the fractions involved have the same denominator. In the next section, we will be looking at adding and subtracting fractions where the denominators are different.
Complete the calculation below.
The denominators of the fraction above are the same. Therefore, we are able to add the numerators together, which gives 5 (3 + 2). The denominator of the fraction remains the same.
Therefore, the answer is 5/7. Whenever we get a fraction as an answer, we need to check that the fraction is in its simplest form. We do this by dividing the numerator and denominator by any common factors between the numerator and the denominator. There are no common factors between 5 and 7, which means that this fraction is already in its simplest form.
Complete the calculation below.
The denominators of the two fractions above are the same. This means that we just minus the second numerator from the first. The numerator for the answer is 4 (11 – 7). The denominator for the answer remains the same, which means that the denominator is 12.
We now need to check whether there are any common factors in the numerator (4) and the denominator (12). There is a common factor of 4. Therefore, we divide both the numerator and denominator of the fraction by 4.
We now check this fraction to see if there are any more common factors. There are no common factors between the numerator (1) and the denominator (3), which means that the fraction is in its simplest form; the answer is 1/3.