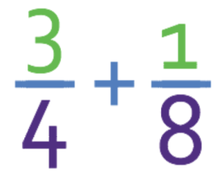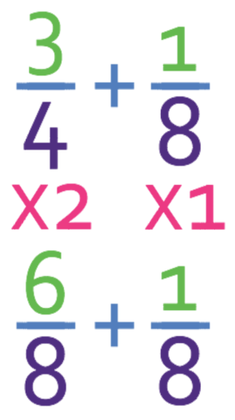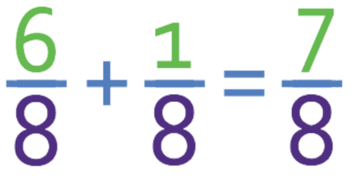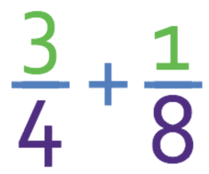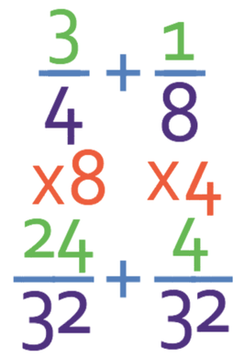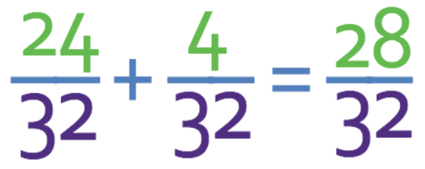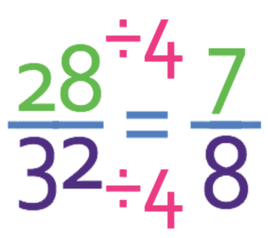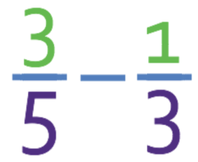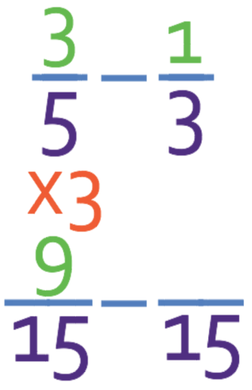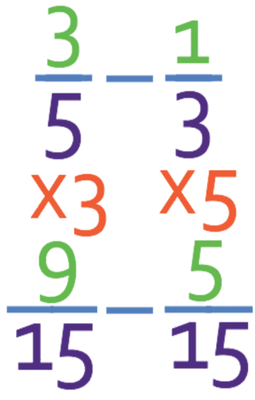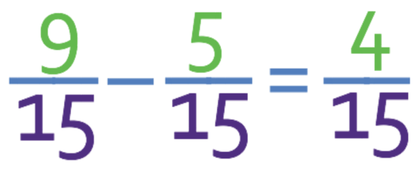1.3 H) Adding & Subtracting Fractions – Part 2
Whenever we are adding or subtracting fractions, we need to ensure that the denominators of the fractions involved are the same. This was the case in the two examples in the previous section (the denominators for the fractions in the first question were 7 and the denominators for the fractions in the second question were 12). As the denominators were the same, we were able to carry out the calculation using the numerators.
If the denominators of the fractions are not the same, we need to create equivalent fractions to the fractions that are in the question with a common denominator. The common denominator for the fractions involved is the lowest common multiple between the denominators for the original fractions (the lowest common multiple is the lowest number that all of the denominators go into).
When we have found a common denominator, we then create equivalent fractions for the fractions in the question. The final step is to carry out the calculation. If we are adding fractions, we add the numerators and keep the denominator the same. If we are subtracting the fractions, we take the numerators and keep the denominator the same.
Let’s suppose that we had two fractions. If you are unsure what the lowest common multiple is between the two denominators of the fractions involved, you can cross multiply. This means that you multiply the numerator and denominator of the first fraction by the denominator of the second fraction, and then you multiply the numerator and denominator of the second fraction by the denominator of the first fraction. This method is useful to use if you are unsure what the lowest common multiple is.
The best way to see how this process works is to have a look at a few examples.
Complete the calculation below.
The denominators of the two fractions above are different, which means that we are unable to add the two fractions. Therefore, the first stage in this question is to create equivalent fractions to those in the calculation that have the same denominator.
Method 1
I am going to use the technique whereby I make the common denominator the lowest common multiple between the two denominators; I am looking for the lowest number that both 4 and 8 go in to. The lowest common multiple between these two numbers is 8. I now need to create equivalent fractions to the ones in the question with denominators of 8. The denominator of the first fraction is 4. In order to make it 8, I need to multiply it by 2. As we are creating equivalent fractions, I need to multiply the numerator and the denominator by 2. This means that the first fraction becomes 6/8. The denominator of the second fraction is 8, which means that we do not need to do anything to this fraction.
The denominators for the two fractions are now the same, which means that I am able to add the numerators.
The final step is to check that the answer is in its simplest form, which it is because there are no common factors between 7 and 8.
Method 2
The second method to obtain the answer was to cross multiply; multiply the numerator and denominator of the first fraction by the denominator of the second fraction, and then you multiply the numerator and denominator of the second fraction by the denominator of the first fraction. The original calculation is given below.
I therefore multiply the numerator and denominator of the first fraction by 8 and the numerator and the denominator of the second fraction by 4.
The denominators of the fractions are the same, which means that we are able to complete the calculation by adding the numerators.
We now need to check that the answer above is in its simplest form, which it is not because there is a common factor of 4 between the numerator and the denominator (4 is the highest common factor between 28 and 32). Therefore, we divide both the numerator and the denominator by 4, which gives us the final answer of 7/8.
You can see that both of these methods give you the same answer, but the first method is faster at obtaining this answer.
Complete the calculation below.
Like the question before, the denominators for the two fractions are not the same. This means that the first step in this question is to create equivalent fractions whereby the denominators of the fractions are the same. A good common denominator to choose is the lowest common multiple between the two current denominators. Therefore, we are looking for the lowest number that 5 and 3 both go in to, which is 15.
We now need to go about creating equivalent fractions that have denominators of 15. The first fraction has a denominator of 5 and in order to get the denominator to equal 15, we need to multiply it by 3. As we are creating equivalent fractions, we need to multiply the numerator by the same number that we multiply the denominator by, which means that we need to multiply the numerator by 3.
We now need to get the denominator of the second fraction to equal 15. Currently the denominator is 3 and to get it to equal 15, we need to multiply by 5. Therefore, we also multiply the numerator by 5.
We now have our two fractions with the same denominators. This means that we can carry out the calculation by subtracting the numerators and keeping the denominator the same.
The final step is to check that the fraction is in its simplest for, which it is because there are no common factors between the numerator and the denominator.
The cross multiplication technique for this question would have worked out exactly the same because the lowest common multiple for 5 and 3 was 15, which is the same denominator that would have been obtained by cross multiplying.