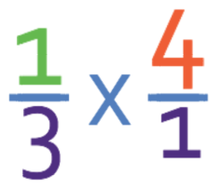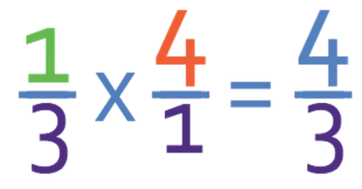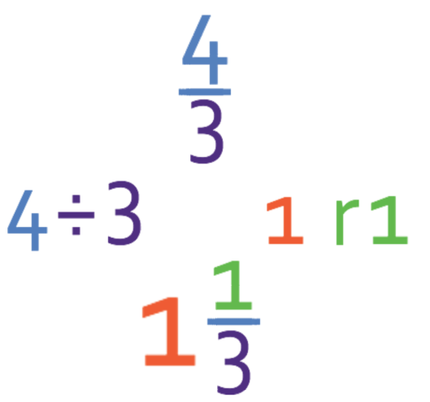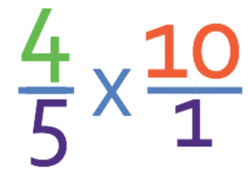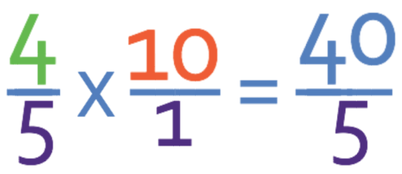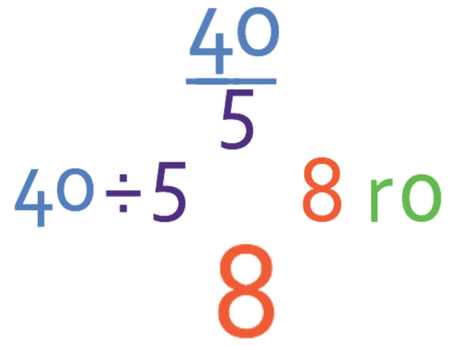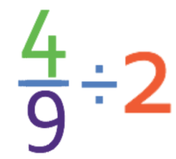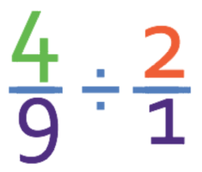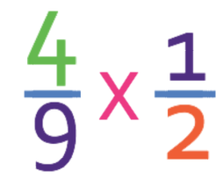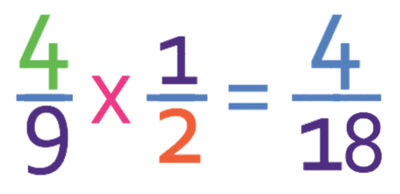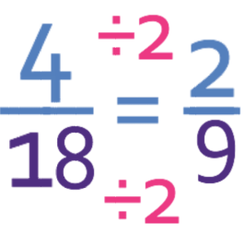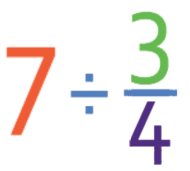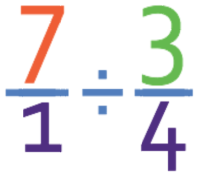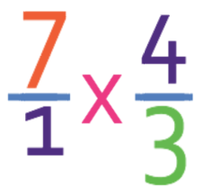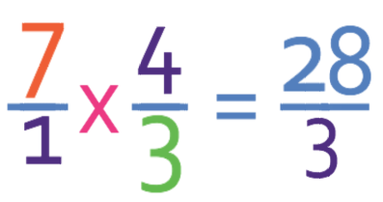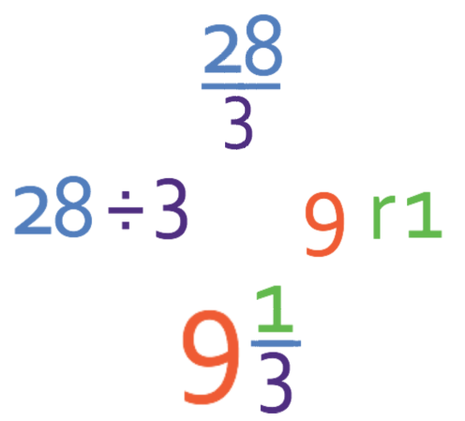1.3 M) Multiplying & Dividing by Whole Numbers
We can represent a whole number as a fraction by having the whole number as the numerator and the denominator as 1. For example, 6 as a fraction is 6/1, 3 as a fraction is 3/1 and finally 35 as a fraction is 35/1.
It is useful to know this especially when we are multiplying or dividing fractions by whole numbers.
When we are multiplying fractions, we multiply the numerator to give us the numerator in the answer and we multiply the denominators to give the denominator in the answer.
When we are dividing fractions, we keep the first fraction the same, flip the second fraction (the fraction we are dividing by) and change the division sign to a multiplication sign. We then multiply across in the same way as discussed above. An easy way to remember this is KFC; Keep the first fraction, Flip the second fraction and Change the sign.
Let’s have a few examples.
Complete the calculation below.
We are multiplying the fraction by 4 and 4 written as a fraction is 4/1. The calculation now becomes.
We now have two numerators and two denominators. Whenever we are multiplying fractions, we multiply the numerators and multiply the denominators.
We now need to convert this improper fraction into a mixed number and check if it can be simplified. To convert it into a mixed number, we see how many times the denominator (3) fully goes into the numerator, which is once with a remainder of 1. Therefore, the mixed number is 1 1/3.
We now check the fraction part of the mixed number to see if it can be simplified, which it cannot because there are no common factors between 1 and 3. This means that the answer to this question is 1 1/3.
Complete the calculation below.
Let’s convert the 10 into a fraction by adding a denominator of 1; 10 written as a fraction is 10/1.
We are now able to multiply straight across.
We now need to check if the equation can be simplified and convert it from an improper fraction into a mixed number. Let’s convert it to a mixed number first and we do this by seeing how many times 5 (the denominator) goes into the numerator (40), which is 8 full times with no remainder. Therefore, the answer to this question is 8.
Complete the calculation below.
The best way to start this question is to make the 2 a fraction, which we do by placing it over 1. The calculation becomes:
We are now able to follow the process of dividing fractions, which is to keep the first fraction the same, flip the second fraction and change the division sign to a multiplication sign.
We now multiply across by multiplying the two numerators and multiplying the two denominators.
We now simplify and convert into a mixed number if applicable. Both the numerator and the denominator are even, which means that they both have a factor of 2. Therefore, we can divide both of them by 2.
There are no more factors between 2 and 9, which means that the fraction is in its simplest form. The numerator of the fraction is less than the denominator, which means that our fraction is a proper one and cannot be converted into a mixed number. The answer to this question is 2/9.
Complete the calculation below.
Let’s start by converting the 7 into a fraction, which we do by having the denominator as 1.
We are now able to follow the normal division technique, which is to keep the first fraction the same, flip the second fraction and changing the sign from a division sign to a multiplication sign.
We now multiply across as usual.
We now check to see if the fraction can be simplified and convert it into a mixed number. This fraction can be converted to a mixed number because it is improper (the numerator is greater than the denominator). We convert it into a mixed number by seeing how many times the denominator goes into the numerator; we divide 28 by 3. This gives us 9 remainder 1. Therefore, the fraction as a mixed number is 9 1/3.
The fraction part of the number is in its simplest form because there are no common factors between the numerator (1) and denominator (3).
The answer to this question is 9 1/3.