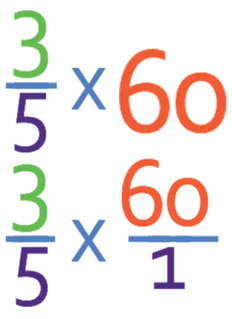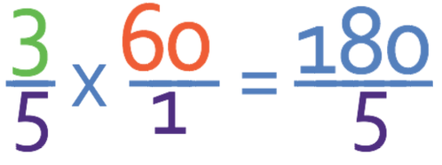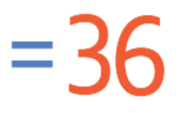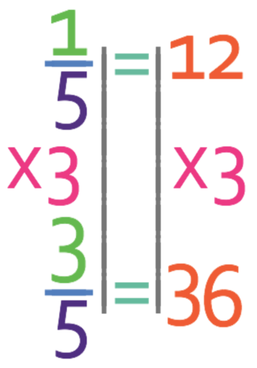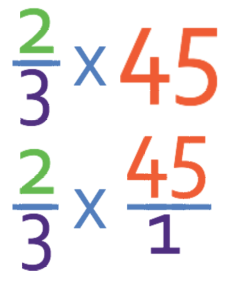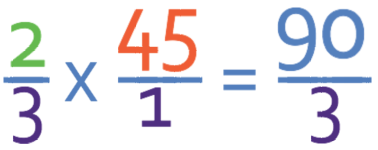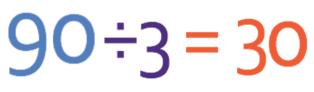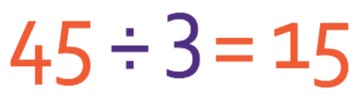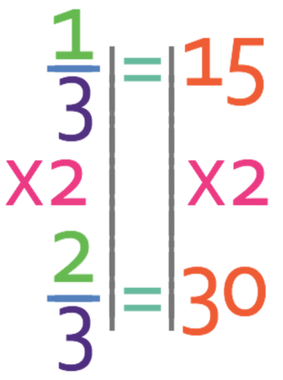1.3 N) Fractions of Amounts – Part 1
There are two different methods that we can use to do this. These methods are:
- Multiplying fractions
- The unitary method
I am going to work through both of these methods in this section, so give both of them a go and see which method you prefer.
What is 3/5 of 60?
Method 1 – Multiplying Fractions
The first works by making both terms a fraction and multiplying the two fractions together. 3/5 is already a fraction, so we only need to make 60 a fraction, which we do by adding a denominator of 1 (a denominator of 1 does not change the answer because anything divided by 1, is itself. Therefore, 60/1 is 60). Our calculation becomes:
We now have two fractions that we are multiplying together. Whenever, we are multiplying fractions, we multiply the two numerators to get the numerator of the answer, and multiply the two denominators to get the denominator of the answer.
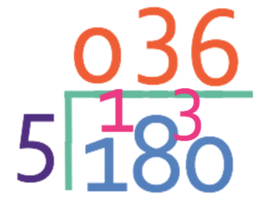
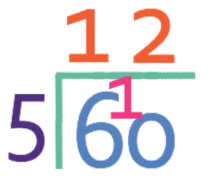
The next step is to simplify and turn the fraction into a mixed number. I am going to turn the fraction above into a mixed number, which we do finding out how many times the denominator goes into the numerator; 180 ÷ 5. We can use the bus stop method to carry out this calculation.
By using the bus stop method, we can see that 5 goes into 180 36 times and there is no remainder. This means that 3/5 of 60 is 36.
Method 2 – The Unitary Method
The best way of understanding the unitary method is to go straight into the question. The question is asking us to find 3/5 of 60. The unitary method works by finding one fifth of 60 and then multiplying by the number of fifths that we want, which is 3 for this example. To find out what one fifth of 60 is, we divide by 5 – again the bus stop method is a good method to choose.
One fifth of 60 is 12. The question is asking us to find three fifths of 60 and this means that we multiply the value for one fifth by 3.
Therefore, 3/5 of 60 is 36, which is the same answer as the method before.
What is 2/3 of 45?
Method 1 – Multiplying Fractions
The first step in the multiplication method is to make the 45 a fraction, which we do by giving it a denominator of 1. The calculation is:
We now multiply straight across.
This is an improper fraction, which means that we need to make the answer a mixed number. We do this by seeing how many times 3 fully goes into 90, and 3 goes into 90 fully 30 times with no remainder. Therefore, 2/3 of 45 is 30.
Method 2 – The Unitary Method
The question is asking us to find 2/3 of 45. The unitary method works by finding what one third is and then multiplying the value for one third by two because we are looking for two thirds.
We obtain the value for one third by dividing the amount (45) by 3. Therefore, one third of 45 is 15.
We are looking for two thirds, so we need to multiply 15 (the value for one third) by 2.
Therefore, 2/3 of 45 is 30.