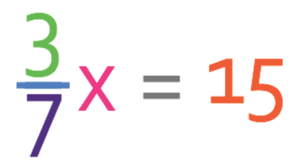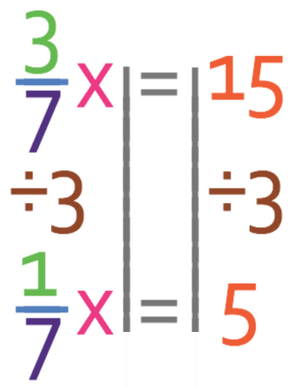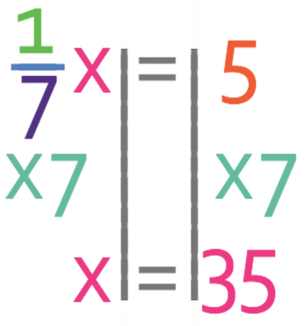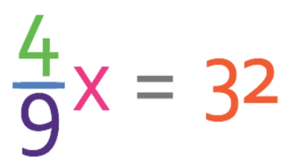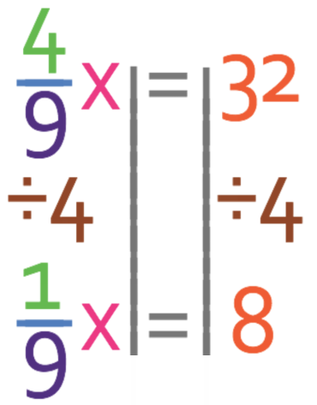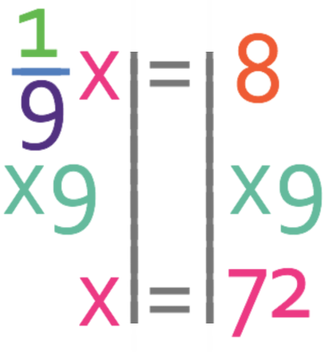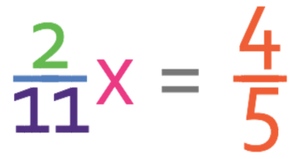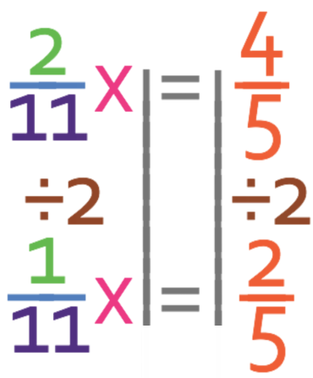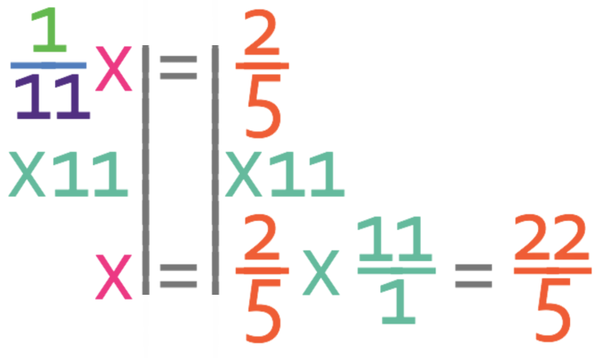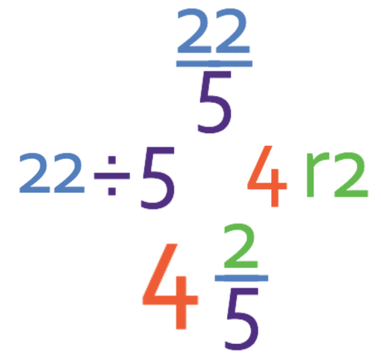1.3 O) Fractions of Amounts – Part 2
Sometimes in the exam you will be asked questions like this; “3/7 of a number is 15, what was the number?”. The easiest way to answer questions like this is to represent the number that we are looking for as an unknown, such as x. We then create an equation where the fraction (in this example 3/7) multiplied by the number (which is x) is equal to 15.
The next step is to get the numerator of the fraction to equal 1. Currently the numerator of the fraction is 3, therefore, we need to divide by 3. As we have an equation, we need to make sure that what we do to one side of the equation, we also do to the other side of the equation. This means that we need to divide both sides of the equation by 3.
We want to find the value of x, but currently we have 1/7 of x. In order to find x, we need to multiply both sides of the equation by the denominator of the fraction. For this example, the denominator of the fraction is 7, therefore, we multiply both sides of the equation by 7.
The number that we are looking for is 35.
4/9 of a number is 32. What is the number?
Like the previous example, the first step in answering this question is to let the number that we are looking for equal x. We know that 4/9 of x is 32 and this means that we can create the equation below.
The next step is to divide both sides by the value of the numerator in the fraction. This means that we are going to divide both sides by 4.
The final step is to multiply both sides of the equation by the denominator of the fraction and this is because we want to find what x is and not what 1/9 of x is. Therefore, we multiply both sides of this equation by 9.
The number that we are looking for is 72.
When we are dividing by the value of the numerator and multiplying by the value of the denominator, we are only doing this for the numerator and the denominator of the fraction of the number that we have (we are only doing this for the fraction that is next to the x). We are now going to have an example whereby we have two fractions.
2/11 of a number is 4/5. What is the value of the number? Give your answer as a mixed number.
The first step is let the number that we are looking for equal x. We know 2/11 of x is 4/5 and this means that we can create the equation that is given below.
We are only interested with the fraction that is next to the x; we do not care about the other fraction (the fraction on the right; 4/5). We now need to get the numerator to become 1, which we do by dividing both sides of the equation by 2.
The next step is to multiply both sides of the equation by the value of the denominator, which in this case is 11. This is because we want to find what the value of x is and currently we have 1/11 of x. When we are multiplying the right side of the equation by 11, you may find it easier to write 11 as 11/1. We then apply the rules for multiplying fractions, which is that you multiply straight across; you multiply both of the numerators together to obtain the numerator for the answer and you multiply both of the denominators together to obtain the denominator for the answer.
This means that x is 22/5. The question asks us to give our answer as a mixed number and currently our answer is an improper fraction because the numerator of the fraction is greater than the denominator. In order to turn our improper fraction into a mixed number, we see how many times the denominator fully goes into the numerator; how many times does 5 fully go into 22. 5 fully goes into 22 4 times with a remainder of 2 (the remainder will be the numerator in the fraction part of the mixed number). Therefore, the number that we are looking for is 4 2/5.