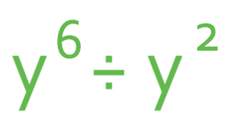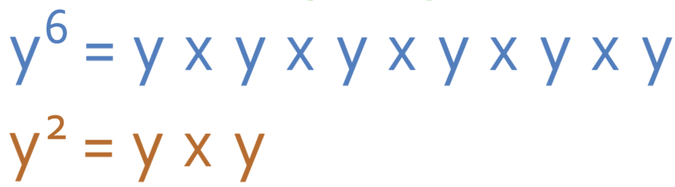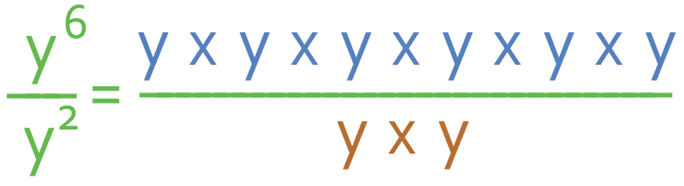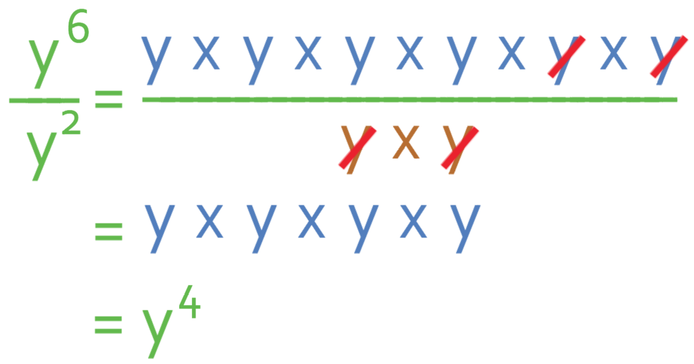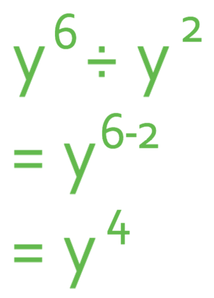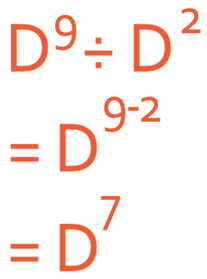1.6 C) Division
When we are dividing powers that have the same base, we take the powers away from each other.
Example 1
Simplify:
Like with multiplication, I am going to write out these indices in full. This gives us:
When we write the question out we get:
We can simplify this fraction because the numerator and the denominator both have y x y (or y2) in common. This leaves the fraction as:
Therefore, the answer to this question is y4.
Now let’s answer the question using the rule. The bases are the same, which means that we can take the powers away from one another.
This gives us the same answer that we got before when we were using the other method.
Example 2
What is:
The bases are the same, which means that we can take the powers away from one another.
As with multiplication, we need to make sure that the bases of the powers are the same because if they are not the same, we will be unable to divide the indices. For example, we would be unable to combine the indices A7 ÷ B6.
We follow the rule for division, even if we have a negative power. We will be looking at what a negative power means later on in this section.