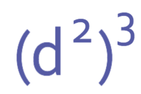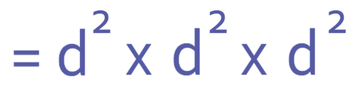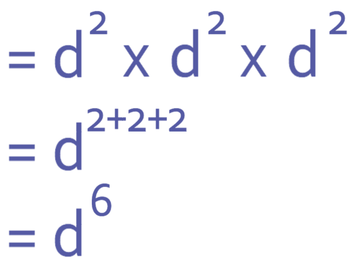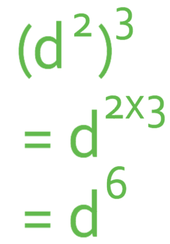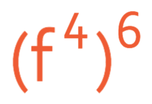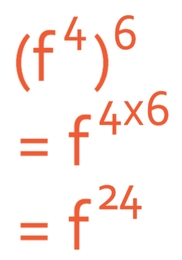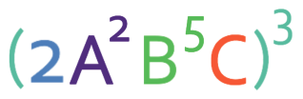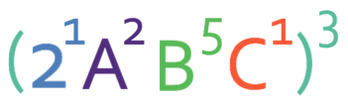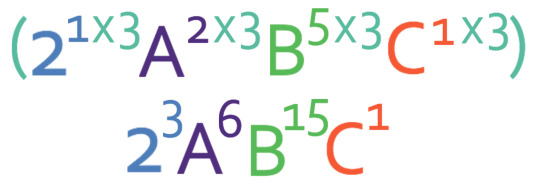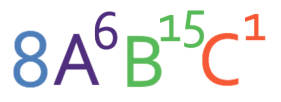1.6 D) Raising a Power to Another Power
When we raise one power to another power, we multiply the powers.
Example 1
Simplify:
We can write this as d2 multiplied by itself 3 times.
When we multiply powers, we add the powers together (providing that they have the same base). In the question above, they all have the same base (d). Therefore, we can add the powers together. This results in the question becoming.
If we use the rule, we can multiply the power within the bracket by the power that is outside the bracket.
This gives us the same answer that we obtained earlier.
The writing of each of the terms out in full was there to show you where the rule comes from/ to prove that the rule works. From now on you can just use the rule, which is that when we raise a power to another power, we multiply the powers.
Example 2
Simplify:
I am going to work this out by using the rule and the rule states that we multiply the powers.
The answer is f24.
Example 3
The final example that we are going to look at is more complex. Simplify:
We answer this question by multiplying all of the powers for each of the four components by the power that is outside the bracket (3).
Before we multiply by the power on the outside of the bracket, I am going to add in a power of 1 for all of the components that do not have a power; I will add a power of 1 for the 2 and the C.
By adding a power of 1, we ensure that we do not forget any terms. It is very common for students to forget to multiply the power for the number.
We now multiply each of the powers for the 4 different components by the power on the outside of the bracket; we multiply each of the powers by 3.
The final step is to write the number out of index form; we need to write 23 as a number. 23 means that we multiply 2 by itself 3 times; 23 = 2 x 2 x 2 = 8. Therefore, our final answer is: