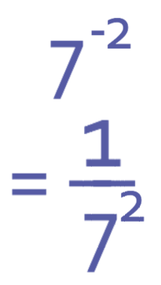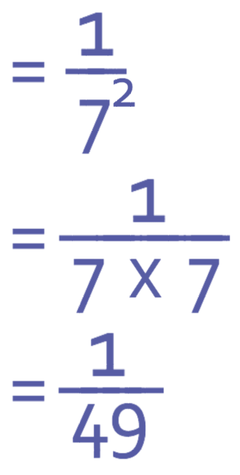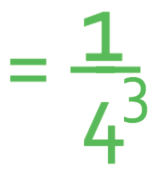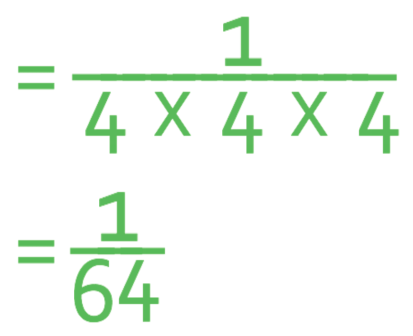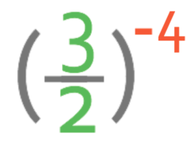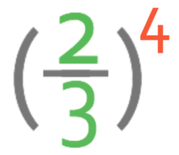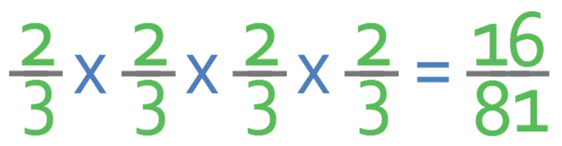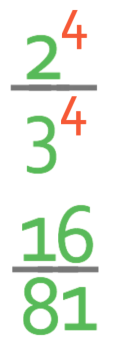1.6 E) Negative Powers
When we have negative powers (e.g. 7-2) we reciprocate it and make the power positive. Reciprocating a number means that we divide 1 by the number. Here are a few examples of numbers/ unknowns and their reciprocals:
> 4 has the reciprocal 1/4
> 10 has the reciprocal 1/10
> 25 has the reciprocal 1/25
> x has the reciprocal 1/x
> 21y has the reciprocal 1/21y
When we reciprocate a fraction, we flip the fraction; the original numerator becomes the new denominator, and the original denominator becomes the new numerator. Here are a few examples:
> 3/4 has the reciprocal 4/3
> 2/7 has the reciprocal 7/2
After we have found the reciprocal for a negative power, we then make the power positive and complete the calculation.
Example 1
What is:
We have a negative power; the power is -2. Therefore, we need to reciprocate it and change the power from a negative to a positive. This gives us:
7 now has a positive power of 2, which means that we square 7.
Therefore, we can write the answer as 1/49.
The key rule with a negative power is to reciprocate it and then change the power to a positive power.
Example 2
What is:
The power is negative (-3), which means that we need to reciprocate this and then make the power positive. This gives us:
The next step is to work out what 43 is, which is 4 multiplied by itself 3 times; 4 x 4 x 4.
The answer is 1/64.
We are now going to have a look at an example whereby we have a fraction to a negative power. We answer questions like this in the same way as all of the previous negative power questions; we reciprocate the base (number or fraction) and change the power from a negative power to a positive power. When we reciprocate a fraction, the original numerator becomes the new denominator, and the original denominator becomes the new numerator.
Example 3
What is:
We have a negative power, so the first step is to flip the fraction and change the power from a negative to a positive power.
There are two different ways that we can finish off the rest of this question.
Way 1
The first way is to multiply the base (2/3) by itself 4 times. When we multiply fractions, we multiply straight across. The working is shown below:
The answer is 16/81
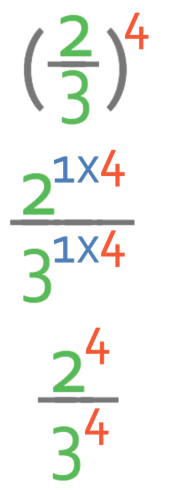
Way 2
The second way is to bring the power outside the bracket (4) in for each of the individual terms. When we raise a power to another power, we multiply the powers together. Currently, the 2 and the 3 have a power of 1. The working is shown below:
The next step is to take each of the numbers out of index form.
The answer is 16/81.
Both of these methods give the same answer, so choose the method that you prefer.